You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 오목 다각형 on Google, you do not find the information you need! Here are the best content compiled and compiled by the https://toplist.maxfit.vn team, along with other related topics such as: 오목 다각형 오목다각형 무게중심, 오목사각형, 볼록사각형, Convex polygon, 오목다면체, 다각형 내각의 합, 정다각형, 다각형이란
어떤 다각형에서 이웃하는 임의의 두 꼭짓점을 잇는 직선에 대하여 나머지 꼭짓점 중에서 적어도 2개가 존재할 경우 이 다각형을 오목다각형이라고 한다.
오목다각형(concave polygon) | 과학문화포털 사이언스올
- Article author: www.scienceall.com
- Reviews from users: 21464
Ratings
- Top rated: 4.5
- Lowest rated: 1
- Summary of article content: Articles about 오목다각형(concave polygon) | 과학문화포털 사이언스올 Updating …
- Most searched keywords: Whether you are looking for 오목다각형(concave polygon) | 과학문화포털 사이언스올 Updating 과학의 모든 것! 과학 학습, 과학 체험, 과학 문화의 모든 것 사이언스올!어떤 다각형에서 이웃하는 임의의 두 꼭짓점을 잇는 직선에 대하여 나머지 꼭짓점 중에서 적어도 2개가 존재할 경우 이 다각형을 오목다각형이라고 한다.오목다각형
- Table of Contents:

오목 다각형 – 위키백과, 우리 모두의 백과사전
- Article author: ko.wikipedia.org
- Reviews from users: 31180
Ratings
- Top rated: 4.6
- Lowest rated: 1
- Summary of article content: Articles about 오목 다각형 – 위키백과, 우리 모두의 백과사전 볼록하지 않은 단순 다각형은 오목, 비볼록 또는 재진입한다고 부른다. 오목 다각형은 항상 최소 하나 이상의 내각이 요각이다. … 요각은 180도와 360도를 제외한 그 사이 … …
- Most searched keywords: Whether you are looking for 오목 다각형 – 위키백과, 우리 모두의 백과사전 볼록하지 않은 단순 다각형은 오목, 비볼록 또는 재진입한다고 부른다. 오목 다각형은 항상 최소 하나 이상의 내각이 요각이다. … 요각은 180도와 360도를 제외한 그 사이 …
- Table of Contents:
참조[편집]
외부 링크[편집]

볼록다각형과 오목다각형 : 네이버 블로그
- Article author: m.blog.naver.com
- Reviews from users: 2457
Ratings
- Top rated: 4.0
- Lowest rated: 1
- Summary of article content: Articles about 볼록다각형과 오목다각형 : 네이버 블로그 볼록다각형과 오목다각형 … 즉, 다각형의 모든 꼭지점이 변을 연장한 직선에 대해 같은 쪽에 있을 때. 이 다각형을 볼록다각형이라 한다. …
- Most searched keywords: Whether you are looking for 볼록다각형과 오목다각형 : 네이버 블로그 볼록다각형과 오목다각형 … 즉, 다각형의 모든 꼭지점이 변을 연장한 직선에 대해 같은 쪽에 있을 때. 이 다각형을 볼록다각형이라 한다.
- Table of Contents:
카테고리 이동
보노군의 블로그
이 블로그
Geometry
카테고리 글
카테고리
이 블로그
Geometry
카테고리 글
도형이 오목 다각형인지 알아보기 – Concave 판단 :: 껍데기방
- Article author: husk321.tistory.com
- Reviews from users: 12021
Ratings
- Top rated: 3.1
- Lowest rated: 1
- Summary of article content: Articles about 도형이 오목 다각형인지 알아보기 – Concave 판단 :: 껍데기방 도형을 크게 2가지로 분류한다면 하나는 일반적으로 볼 수 있는 볼록 다각형과 오목하게 들어가있는 오목 다각형이 있습니다. 오목 다각형의 경우 … …
- Most searched keywords: Whether you are looking for 도형이 오목 다각형인지 알아보기 – Concave 판단 :: 껍데기방 도형을 크게 2가지로 분류한다면 하나는 일반적으로 볼 수 있는 볼록 다각형과 오목하게 들어가있는 오목 다각형이 있습니다. 오목 다각형의 경우 … 서론 도형을 크게 2가지로 분류한다면 하나는 일반적으로 볼 수 있는 볼록 다각형과 오목하게 들어가있는 오목 다각형이 있습니다. 오목 다각형의 경우 내각들 중 하나라도 180도를 넘어가는 각이 있다면 오목..
- Table of Contents:
관련글 관련글 더보기
인기포스트
티스토리툴바
오목 다각형
- Article author: allthatmath.com
- Reviews from users: 6496
Ratings
- Top rated: 3.2
- Lowest rated: 1
- Summary of article content: Articles about 오목 다각형 오목 다각형과 볼록 다각형? 17.jpg 다각형이란 꼭짓점을 선분으로 연속적으로 연결하였을 때, 이들 선분으로 둘러싸인 도형이다. 따라서 원이나 … …
- Most searched keywords: Whether you are looking for 오목 다각형 오목 다각형과 볼록 다각형? 17.jpg 다각형이란 꼭짓점을 선분으로 연속적으로 연결하였을 때, 이들 선분으로 둘러싸인 도형이다. 따라서 원이나 …
- Table of Contents:

‘오목다각형’ là gì?, Từ điển Tiếng Hàn
- Article author: vi.vdict.pro
- Reviews from users: 41645
Ratings
- Top rated: 3.1
- Lowest rated: 1
- Summary of article content: Articles about ‘오목다각형’ là gì?, Từ điển Tiếng Hàn Nghĩa của từ 오목다각형 trong Từ điển Tiếng Hàn 오목 다각형(―多角形)[―따가켱][명사]다각형의 한 변이나 여러 변을 연장할 때, 그 변이 그 도형 안을 통과하는 … …
- Most searched keywords: Whether you are looking for ‘오목다각형’ là gì?, Từ điển Tiếng Hàn Nghĩa của từ 오목다각형 trong Từ điển Tiếng Hàn 오목 다각형(―多角形)[―따가켱][명사]다각형의 한 변이나 여러 변을 연장할 때, 그 변이 그 도형 안을 통과하는 … Nghĩa của từ 오목다각형 trong Từ điển Tiếng Hàn 오목 다각형(―多角形)[―따가켱][명사]다각형의 한 변이나 여러 변을 연장할 때, 그 변이 그 도형 안을 통과하는 다각형. ↔볼록 다각형.
- Table of Contents:

어떤 다각형이 오목 다각형인지 판별하는 방법 – License
- Article author: sites.google.com
- Reviews from users: 37692
Ratings
- Top rated: 4.8
- Lowest rated: 1
- Summary of article content: Articles about 어떤 다각형이 오목 다각형인지 판별하는 방법 – License 오목(concave) 다각형 : 180º 이상인 내각이 존재함 (볼록하지 않은 다각형). 볼록 다각형과 오목 다각형의 판별. 꼭짓점을 와인딩 순서에 따라 연결 … …
- Most searched keywords: Whether you are looking for 어떤 다각형이 오목 다각형인지 판별하는 방법 – License 오목(concave) 다각형 : 180º 이상인 내각이 존재함 (볼록하지 않은 다각형). 볼록 다각형과 오목 다각형의 판별. 꼭짓점을 와인딩 순서에 따라 연결 … 잡지식
- Table of Contents:

지금까지 이런 수학은 없었다: 수포자였던 수학 교사, 중학 수학의 새로운 접근법 … – 이성진 – Google Sách
- Article author: books.google.com.vn
- Reviews from users: 5488
Ratings
- Top rated: 4.5
- Lowest rated: 1
- Summary of article content: Articles about 지금까지 이런 수학은 없었다: 수포자였던 수학 교사, 중학 수학의 새로운 접근법 … – 이성진 – Google Sách Updating …
- Most searched keywords: Whether you are looking for 지금까지 이런 수학은 없었다: 수포자였던 수학 교사, 중학 수학의 새로운 접근법 … – 이성진 – Google Sách Updating “수학을 포기하려는 학생들의 눈높이에서 바라봤더니,중학 수학에 변화가 필요하다는 사실을 깨달았다.”현직 수학 교사가 10년에 걸쳐 발견한 새로운 수학 풀이법!한때 ‘수포자’였던 현직 수학 교사가 치열하게 고민한 끝에 발견한 중학 수학의 새로운 접근법이 담긴 책이다. 계산보다는 이해, 결과보다는 과정 그리고 창의성에 초점을 두고 수학에 접근해야 한다는 표어 아래, 학생들이 어려워하는 개념을 누구나 이해할 수 있는 수준으로 쉽게 설명하고, 학생들이 자신만의 창의적인 풀이를 이끌어내도록 유도한다. 『지금까지 이런 수학은 없었다』의 새로운 시도는 학생들이 풀이 방법을 외워 문제를 푸는 ‘계산 기계’에서 벗어나, 개념을 제대로 이해하고 수학적 사고력까지 갖춘 ‘수학 능력자’로 향하도록 안내하는 훌륭한 길잡이가 될 것이다.
- Table of Contents:
탈레스가 들려주는 평면 도형 이야기: 과학자가 들려주는 과학 이야기 099 – 홍선호 – Google Sách
- Article author: books.google.com.vn
- Reviews from users: 4787
Ratings
- Top rated: 4.2
- Lowest rated: 1
- Summary of article content: Articles about 탈레스가 들려주는 평면 도형 이야기: 과학자가 들려주는 과학 이야기 099 – 홍선호 – Google Sách Updating …
- Most searched keywords: Whether you are looking for 탈레스가 들려주는 평면 도형 이야기: 과학자가 들려주는 과학 이야기 099 – 홍선호 – Google Sách Updating 과학자가 독자들에게 자신의 과학 이야기를 설명하는 형식으로 구성한 「과학자가 들려주는 과학 이야기」 시리즈 제97권 『아인슈타인이 들려주는 상대성 이론 이야기』. 지적 호기심을 자극하는 흥미로운 실험과 이를 설명하는 이론들을 초등학생 및 중학생들이 이해할 수 있도록 쉬우면서도 논리적으로 설명한 책이다. 이로부터 과학에 대한 깊은 이해와 이를 발견해낸 과학자들의 창의적인 사고과정을 체득할 수 있다.
- Table of Contents:
See more articles in the same category here: toplist.maxfit.vn/blog.
위키백과, 우리 모두의 백과사전
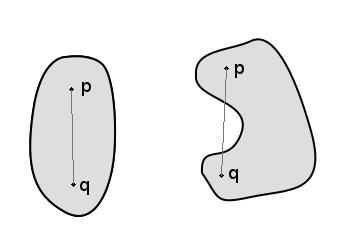
오목 다각형의 예시이다.
볼록하지 않은 단순 다각형은 오목,[1] 비볼록[2] 또는 재진입[3]한다고 부른다. 오목 다각형은 항상 최소 하나 이상의 내각이 요각이다.[4] 요각은 180도와 360도를 제외한 그 사이의 각을 의미한다.
오목 다각형의 내부의 점을 포함하는 어떤 선은 그 다각형의 경계를 두 점보다 많이 교차한다.[4] 오목 다각형의 어떤 대각선은 일부나 전체가 다각형 외부에 위치한다.[4] 오목 다각형의 어떤 확장된 변은 평면을 한쪽에 다각형이 완전히 있는 두 반평면으로 분리할 수 없다. 이 세 문장이 성립하지 않으면 볼록 다각형이다.
많은 단순 다각형에서, 오목 다각형의 내각의 합은 π (n − 2) 라디안 또는 180°×(n − 2)이다. 이 때, n은 변의 개수이다.
오목 다각형을 볼록 다각형의 집합으로 분할 하는 것은 항상 가능하다. 가능한한 적은 수의 볼록 다각형으로의 분할을 찾는 다항 시간 알고리즘은 Chazelle & Dobkin (1985)에 의해 설명되었다.[5]
삼각형은 오목해질 수 없지만, 모든 n > 3에 대해서 변이 n개인 오목 다각형은 존재한다. 오목한 사각형의 예시는 다트이다.
최소한 한 내각은 다른 모든 꼭짓점을 그 변과 내부에 포함할 수 없다.
오목 다각형의 꼭짓점과 변의 볼록 폐포는 다각형의 외부에 있는 점을 포함한다.
참조 [ 편집 ]
볼록다각형과 오목다각형
도형 혹은 그 내부의 임의의 두 점을 골랐을 때
둘을 연결하는 선분이 도형의 외부와 만나지 않을 경우
이 도형을 볼록집합이라고 한다.
볼록집합인 다각형의 내각은 180도보다 작다.
변을 늘린 직선이 도형의 안으로 들어가지 않을 때,
즉, 다각형의 모든 꼭지점이 변을 연장한 직선에 대해 같은 쪽에 있을 때
이 다각형을 볼록다각형이라 한다.
볼록다각형의 내부는 꼭지점이 있는 반평면의 교집합으로 정한다.
반평면은 볼록집합이므로 볼록다각형도 볼록집합이다.
볼록다각형의 내각의 크기는 180도보다 작다.
만약 180도보다 큰 각이 있다면
그 각의 변을 이은 선분은 도형 외부로 나간다.
즉, 180도 초과이면 이웃한 변이 내부를 뚫는다.
볼록다각형의 대각선의 갯수는 {n(n-3)}/2 이다.
n각형의 한 꼭지점에서 그을 수 있는 대각선의 갯수는 n-3이고
n개의 꼭지점에서는 모두 n(n-3)개의 대각선을 그을 수 있는데
이것은 한 대각선을 두 번씩 계산한 것이므로 대각선의 갯수는
{n(n-3)}/2
이다.
볼록다각형의 각 꼭지점은 각의 내부에 있다.
볼록다각형의 내부는 볼록집합이다.
따라서 볼록다각형의 대각선은
양 끝점을 제외하고 다각형의 내부를 지난다.
볼록다각형을 대각선을 따라 삼각형과 다른 도형으로 잘랐을 때
다른 도형은 닫힌 곡선(시작과 끝이 같은 곡선)이다.
볼록다각형의 양 끝점을 제외한 대각선은 도형의 내부를 지난다.
따라서 이 대각선은 다른 경계와 만나지 않는다.
그러므로 이 도형은 단일폐곡선(겹치지 않는 닫힌 곡선)이다.
각각의 변의 각은 0도나 180도가 아니다.
따라서 이웃한 변은 한 직선 위에 있지 않다.
그러므로 이 도형은 다각형이다.
볼록다각형의 내각의 합은 180(n-2)이다.
왜냐하면 볼록다각형은 한 꼭지점에서 그은 대각선에 의해
n-2개의 삼각형으로 나누어진다.
그런데, 삼각형의 내각의 합은 180이므로
볼록다각형의 내각의 합은 180(n-2)이다.
도형이 오목 다각형인지 알아보기 – Concave 판단
728×90
서론
도형을 크게 2가지로 분류한다면 하나는 일반적으로 볼 수 있는 볼록 다각형과 오목하게 들어가있는 오목 다각형이 있습니다. 오목 다각형의 경우 내각들 중 하나라도 180도를 넘어가는 각이 있다면 오목 다각형이 됩니다. 이를 영어로 Concave Polygon이라고 하는데 그래픽스에서 혹시나 이런 도형들이 있다면 다루기가 복잡하기 때문에 일반적인 Convex(볼록) Polygon으로 만들어줘야 합니다.
그래서 이번 글에서는 혹시나 Concave Polygon이 있다고 하면 이를 어떻게 판단하는지, 어떻게 처리할 것인지 정하는 방법들을 공부한 뒤 정리해 보았습니다.
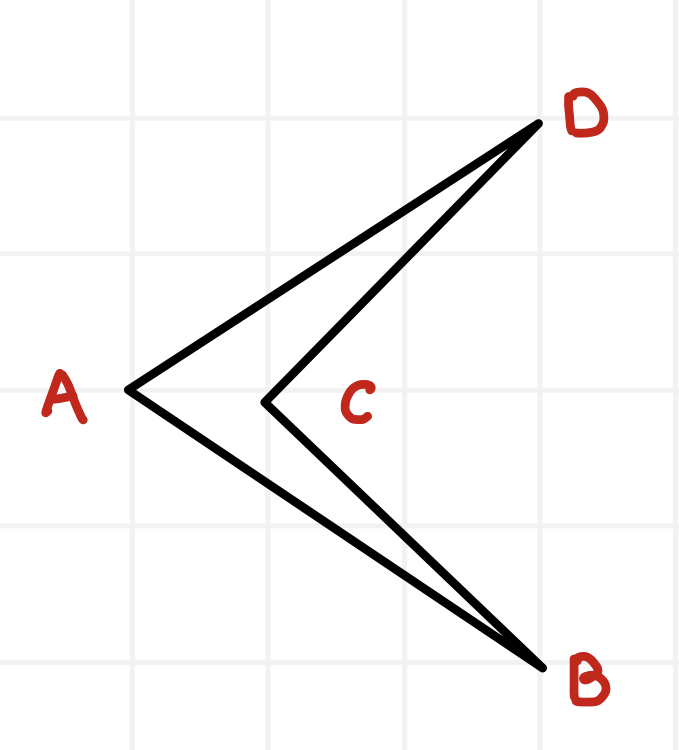
Concave Polygon판단하기
위와 같은 식으로 오목 다각형이 있다고 하면 벡터들의 외적을 통해서 구분이 가능하게 됩니다. 반시계 방향으로 벡터의 방향을 지정해주면(시계방향으로도 가능) A ⇀ B, B ⇀ C, C ⇀D, D ⇀A로 총 4개의 벡터가 나오게 됩니다. 각각 번호를 E1,2,3,4 라고 지정을 해 주면 (E1 X E2), (E2 X E3), (E3 X E4), (E4 X E1)을 했을 때 부호가 다른 결과가 나오게 됩니다.
이 벡터들의 외적의 부호들이 전부 같으면 이 도형은 Convex, 다르다면 Concave임을 판단할 수 있게 됩니다. 이는 벡터의 외적의 결과가 벡터들의 크기의 곱과 sinθ 의 곱으로 이루어져 있기 때문입니다.
Concave 도형 잘라서 Convex로 만들어주기
1. 위 결과에서 벡터를 사용하기
400
일단 위 도형에서 벡터의 외적을 해본다면 B ⇀ C, C ⇀D의 곱 즉, E2 X E3에서 음수의 결과값이 나오게 됩니다. 이때 음수의 결과값이 나온 경우에서 좌항의 벡터를 연장해 도형을 잘라 도형을 2개로 쪼개게 됩니다.
다만 이 방법 후에 다시 Concave한 부분이 있을 수 있으니 결과물들에 대해서 한번 더 Convex 인지 판단을 해 줘야 합니다.
2. Rotational 메소드
점 하나를 원점에 두고 다음 vertex를 X 축 위에 둬서 이 축을 벗어나는 부분을 자르는 알고리즘입니다.
Convex(볼록 다각형)은 처리 과정이 너무 귀찮다
위 과정만 보더라도 볼록 다각형의 경우 처리 과정이 복잡해집니다. 또한 4개 이상의 점을 가지게 되면 이게 한 평면에 있는지 알 수 없어서(non-planar인 도형) 이것까지 전부 처리하면 한 화면 내에서 오브젝트가 많아질수록 속도 저하가 심해질 것입니다.
그래서 보통의 경우 도형을 전부 삼각형으로 나누어서 처리를 한다고 합니다.
728×90
So you have finished reading the 오목 다각형 topic article, if you find this article useful, please share it. Thank you very much. See more: 오목다각형 무게중심, 오목사각형, 볼록사각형, Convex polygon, 오목다면체, 다각형 내각의 합, 정다각형, 다각형이란
