You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 회귀 란 on Google, you do not find the information you need! Here are the best content compiled and compiled by the https://toplist.maxfit.vn team, along with other related topics such as: 회귀 란 회귀하다 뜻, 선형 회귀란, 회귀 한자, 회귀모델이란, 회귀물 뜻, 회귀분석 뜻, 머신러닝 회귀란, 딥러닝 회귀 란
회귀 모델에서 ‘회귀’란 무엇인가?
- Article author: brunch.co.kr
- Reviews from users: 12892
Ratings
- Top rated: 3.6
- Lowest rated: 1
- Summary of article content: Articles about 회귀 모델에서 ‘회귀’란 무엇인가? 회귀의 사전적 정의는 ‘한바퀴 돌아 제자리로 돌아가다’ 입니다. 따라서 회귀 모델에서 말하는 ‘회귀’의 의미를 이해하려면 무엇이 어디로 회귀하는 … …
- Most searched keywords: Whether you are looking for 회귀 모델에서 ‘회귀’란 무엇인가? 회귀의 사전적 정의는 ‘한바퀴 돌아 제자리로 돌아가다’ 입니다. 따라서 회귀 모델에서 말하는 ‘회귀’의 의미를 이해하려면 무엇이 어디로 회귀하는 … Tribute to error | 페이스북에서 ‘regression model에서 regression 이라는 용어는 잘못되었다’ 는 글(https://www.facebook.com/dgtgrade/posts/1153483458043852) 를 봤습니다. 우선 ‘회귀(regression)’ 라는 단어가 일상에서 잘 안쓰이는 단어이고 직관적이지 못하다는 점은 저도 공감합니다. 수학이나 과학 용
- Table of Contents:

회귀란?
- Article author: jaaamj.tistory.com
- Reviews from users: 34455
Ratings
- Top rated: 3.2
- Lowest rated: 1
- Summary of article content: Articles about 회귀란? 회귀는 여러개의 독립변수와 한 개의 종속변수 간의 상관관계를 모델링하는 기법을 의미합니다. 예를들면 아파트의 방 개수, 화장실 크기 등의 독립 … …
- Most searched keywords: Whether you are looking for 회귀란? 회귀는 여러개의 독립변수와 한 개의 종속변수 간의 상관관계를 모델링하는 기법을 의미합니다. 예를들면 아파트의 방 개수, 화장실 크기 등의 독립 … 회귀란?? 회귀는 여러개의 독립변수와 한 개의 종속변수 간의 상관관계를 모델링하는 기법을 의미합니다. 예를들면 아파트의 방 개수, 화장실 크기 등의 독립변수에 따라서 아파트 가격인 종속변수가 어떤 관계를..
- Table of Contents:
공부합시다
회귀란 본문
회귀란
단순 선형 회귀
경사 하강법(Gradient Descent)
티스토리툴바

회귀란?
- Article author: john-analyst.medium.com
- Reviews from users: 28383
Ratings
- Top rated: 4.3
- Lowest rated: 1
- Summary of article content: Articles about 회귀란? 회귀(regression)란. 통계학에서 회귀란, 여러 개의 독립변수와 한 개의 종속변수 간의 상관관계를 모델링하는 기법을 통칭한다. 예를 들어 아파트 방 개수, 크기, … …
- Most searched keywords: Whether you are looking for 회귀란? 회귀(regression)란. 통계학에서 회귀란, 여러 개의 독립변수와 한 개의 종속변수 간의 상관관계를 모델링하는 기법을 통칭한다. 예를 들어 아파트 방 개수, 크기, … 회귀란?? 회귀는 여러개의 독립변수와 한 개의 종속변수 간의 상관관계를 모델링하는 기법을 의미합니다. 예를들면 아파트의 방 개수, 화장실 크기 등의 독립변수에 따라서 아파트 가격인 종속변수가 어떤 관계를..
- Table of Contents:
공부합시다
회귀란 본문
회귀란
단순 선형 회귀
경사 하강법(Gradient Descent)
티스토리툴바

회귀 (Regression)란?
- Article author: velog.io
- Reviews from users: 24962
Ratings
- Top rated: 3.1
- Lowest rated: 1
- Summary of article content: Articles about 회귀 (Regression)란? 회귀는 회귀 계수의 선형/비선형 여부, 독립변수의 개수, 종속변수의 개수에 따라 여러가지 유형으로 나눌 수 있다. 회귀에서 가장 중요한 것은 회귀 계수 … …
- Most searched keywords: Whether you are looking for 회귀 (Regression)란? 회귀는 회귀 계수의 선형/비선형 여부, 독립변수의 개수, 종속변수의 개수에 따라 여러가지 유형으로 나눌 수 있다. 회귀에서 가장 중요한 것은 회귀 계수 … 회귀 개념
- Table of Contents:
회귀(regression)란 무엇인가?
- Article author: philosopher-chan.tistory.com
- Reviews from users: 36337
Ratings
- Top rated: 4.7
- Lowest rated: 1
- Summary of article content: Articles about 회귀(regression)란 무엇인가? 선현 회귀는 종속 변수 y 와 한 개 이상의 독립 변수 x와의 선형 상관 관계를 모델링하는 회귀분석 기법이다. 한 개의 설명 변수에 기반하는 경우는 … …
- Most searched keywords: Whether you are looking for 회귀(regression)란 무엇인가? 선현 회귀는 종속 변수 y 와 한 개 이상의 독립 변수 x와의 선형 상관 관계를 모델링하는 회귀분석 기법이다. 한 개의 설명 변수에 기반하는 경우는 … 머신러닝을 하다보니 회귀(regression)이라는 말이 나옵니다. 그런데 회귀를 잘 설명하지 않고 회귀 모델은 어쩌고 하면서 설명을 하기 때문에, 회귀에 대한 개념이 부족합니다. 회귀에 대한 설명을 찾아보면 선..contact : [email protected]
- Table of Contents:

로지스틱 회귀란 무엇입니까? | 팁코 소프트웨어
- Article author: www.tibco.com
- Reviews from users: 20808
Ratings
- Top rated: 3.7
- Lowest rated: 1
- Summary of article content: Articles about 로지스틱 회귀란 무엇입니까? | 팁코 소프트웨어 로지스틱 회귀란 무엇입니까? · 이진 로지스틱 회귀: 여기서 범주형 응답에 대해 가능한 결과는 두 가지뿐입니다. · 다항 로지스틱 회귀: 여기에는 응답 변수에 순서가 없는 … …
- Most searched keywords: Whether you are looking for 로지스틱 회귀란 무엇입니까? | 팁코 소프트웨어 로지스틱 회귀란 무엇입니까? · 이진 로지스틱 회귀: 여기서 범주형 응답에 대해 가능한 결과는 두 가지뿐입니다. · 다항 로지스틱 회귀: 여기에는 응답 변수에 순서가 없는 … 로지스틱 회귀는 이벤트가 발생할 확률을 결정하는 데 사용되는 통계 모델입니다. 특성 간의 관계를 보여주고 특정 결과의 확률을 계산합니다.
- Table of Contents:
Customers
Solutions
Products
Partners
Engage
Company
Customers
Solutions
Products
Partners
Engage
Company
로지스틱 회귀에 사용되는 가정
로지스틱 회귀의 적용
로지스틱 회귀 분석의 장점과 단점

미국의 아시아 회귀 전략: 미국의 전문가 15인에게 묻는다 – 이용인, 테일러 워시번 – Google Sách
- Article author: books.google.com.vn
- Reviews from users: 4135
Ratings
- Top rated: 4.0
- Lowest rated: 1
- Summary of article content: Articles about 미국의 아시아 회귀 전략: 미국의 전문가 15인에게 묻는다 – 이용인, 테일러 워시번 – Google Sách Updating …
- Most searched keywords: Whether you are looking for 미국의 아시아 회귀 전략: 미국의 전문가 15인에게 묻는다 – 이용인, 테일러 워시번 – Google Sách Updating 중국의 대국굴기(大國崛起)에 따른 주변국 정세의 변화, 천안함사건과 북한의 3차 핵실험으로 인한 한반도의 긴장 고조, 일본의 집단자위권 해석 문제로 인한 한중과의 갈등, 중국-러시아의 신(新)밀월 관계 등 미국의 오바마 행정부 2기 출범 이후 아시아태평양 지역의 정세는 격랑에 휩싸여 그 출구를 가늠하기 힘든 상황에 처했다. 그 시작을 버락 오바마 대통령이 2011년 발표한 ‘아시아 회귀(Pivot to Asia)’ 전략에서부터 짚어보고자 한다. 미국의 총체적 동아시아 외교안보 전략이라 할 수 있는 ‘아시아 회귀 전략’은 아시아태평양 지역을 미 외교정책의 중추로 삼고 있다. 이 정책은 새로운 패권국으로 부상 중인 중국과의 관계에는 물론 한반도 정세 및 동아시아 여러 국가에 미칠 영향력 탓에 지대한 관심과 우려의 대상이 되고 있다.『미국의 아시아 회귀 전략: 미국의 전문가 15인에게 묻는다』는 미국의 아시아 정책을 결정하는 백악관 및 국무부 전‧현직 고위관료, 정책 생산의 핵심중추인 싱크탱크 전문가와 학자 15인에게서 미국의 본심을 직접 묻고 캐낸 책이다. ‘아시아 회귀’ 정책의 실질적 입안자인 커트 캠벨, 미중관계에 탁월한 해법을 제시한 제임스 스타인버그 등 지금까지 국내 언론이 접촉하기 어려웠던 인물들은 물론 차기 동아태 차관보로 점쳐지는 리처드 부시, 쑤전 셔크 등 미국 내 아시아 전략 관련 최고위층 인사와 정치 스펙트럼이 상이한 여러 학자들의 견해를 고루 담아 ‘아시아 회귀’ 전략의 배경과 의의를 중심으로 미중관계의 향방과 그것이 향후 한반도와 동아시아 국가들에 미칠 영향력을 전망해본다. 미국은 왜 아시아로 회귀하려 하는가 : 중국과의 대결과 충돌을 앞두고 벌인 격론 한반도를 둘러싼 국제 정세의 지각판이 움직이고 있다. 소련의 붕괴로 야기된 탈냉전 이후 미국에 필적할 만한 잠재적인 대항세력은 없는 듯했다. 그러나 2000년 이후 중국의 부상은 점차 가시화된 반면, 2008년 금융위기와 이라크·아프가니스탄 전쟁의 장기화로 미국의 헤게모니적 지위는 도전받게 되었다. 2009년 말부터 시작된 중국의 공격적인 행동과 이에 대한 미국의 대응으로 미중관계는 2010년 심각한 고비를 맞기도 했다. 이에 버락 오바마 미 대통령은 2011년 11월 아시아태평양경제공동체(APEC) 및 동아시아 정상회의(EAS) 참석을 계기로 미국의 총체적 동아시아 외교안보 전략이라고 할 수 있는 ‘아시아 회귀’(Pivot to Asia) 전략을 발표한다. 아시아태평양(이하 아태) 지역을 향후 미 대외정책의 중추로 삼겠다는 의미라고는 하나, 군사적 측면에서 보면 대(對)중국적 성격이 짙다. 동아시아 국가들을 대중국 블록 네트워크의 외교적·군사적 거점으로 재조정하고, 중국의 군사전략에 대한 지침도 구체적으로 내놓았기 때문이다. 중국 역시 군사력을 현대화하며 ‘창’을 가다듬고, 미중 간 협조적 관계를 강조하는 ‘신형 대국관계론’이라는 ‘방패’를 마련하는 등 미국의 ‘아시아 회귀’ 전략에 대응하고 있다. 이 책의 제1부(미국의 ‘아시아 회귀 전략’ 논쟁)에서는 힐러리 클린턴 전 국무장관의 ‘오른팔’로 회귀 정책의 실질적인 입안자인 커트 캠벨의 인터뷰를 시작으로 오바마 행정부가 ‘아시아 회귀’를 선언하게 된 배경과 구체적 내용 및 이에 대한 찬반양론을 살펴본다. 중국에 우호적인 대표 학자로 꼽히는 데이비드 램프턴과 2008년 미 대선 당시 ‘오바마의 저격수’로 활동한 미국기업연구소(AEI)의 댄 블루멘설 모두 ‘아시아 회귀 전략’에는 비판적인 입장을 보이나 그 근거는 상이하다. 특히 강경한 대중정책을 지지하는 블루멘설은 중동이나 아프가니스탄에 대한 미국의 이해관계가 여전하며, 중동에 대한 중국의 영향력이 증가하고 있어 이에 실질적으로 대응해야 한다고 주장한다. 또한 그는 아시아 회귀 전략은 반드시 대중봉쇄를 목표로 하고, 보다 많은 자원을 투입할 필요가 있다는 강경파의 주장을 대변한다. 폐쇄적인 워싱턴 정치가에 거침없이 독설을 가하는 ‘돈 끼호떼’형 학자인 저스틴 로건 역시 회귀 전략에 반대하며 각국의 안보는 각자에 맡기고 미국은 아시아가 아니라 ‘미국으로 회귀’(Pivot to Home)해야 한다고 일침을 놓는다. 제2부(미중관계의 현황과 해법)에서는 아시아 회귀 전략의 실체와 향방을 가늠할 미국-중국 관계에 대한 여러 전망과 해법들을 다양한 관점에서 진단해보고자 한다. 국무부 부장관으로 재직할 당시 오바마-힐러리 간 권력 관계의 축을 맡았던 제임스 스타인버그는 보다 강하고 협력적인 미중관계 구축에 전념해야 한다고 보고 이를 저해하는 불신을 해결할 방법으로 ‘전략적 보증’을 제안한다. 백악관 국가안보회의(NSC)에 근무하며 소련의 붕괴와 톈안먼사건을 지켜본 더글러스 팔과는 현재 미중 간 문제가 되는 요소들을 4T, 즉 톈안먼(Tiananmen), 대만(Taiwan), 티베트(Tibet), 무역(Trade)의 영역에서 진단해본다. 동북아시아협력대화(NEACD)를 창립한 쑤전 셔크와는 동북아시아 문제 해결에 다자기구의 유용성을 짚어본다. 마지막으로 미중 간 ‘전략적 불신’ 문제에 집중해온 브루킹스연구소의 케네스 리버설은 다양한 층위의 대화와 교류, 특히 최고위 지도층 간의 인간적 유대 등을 강조했다. 한반도 문제의 외재화에 대비하라 : 매파적 관여에서부터 친중국 드라이브까지 미국의 ‘아시아 회귀’ 전략 이후 강도가 높아진 미국과 중국의 ‘친구 만들기’ 경쟁은 동아시아 각국을 선택의 딜레마로 빠져들게 하고 있다. 상당수 동아시아 국가들이 안보는 미국에, 경제는 중국에 의존하고 있기 때문이다. 동북아시아에서 지정학적 요충지인 한국은 이미 미국의 ‘아시아 회귀’ 전략의 영향권으로 깊숙이 편입되고 있다. 동맹국 및 우호국 들을 네트워크로 연결하고, 이들에게 역할을 전이하는 역량동원 전략 차원에서 미국은 한국에 미사일 방어 시스템(MD) 가입을 공개적으로 요구하고 있다. 하지만 한국이 미국 쪽 네트워크에 편입될수록 한중 간 외교적 마찰은 잦아지고 깊어질 것이다. 또한 아태 지역에서 미중관계의 구심력이 커진다는 것은 결국 개별 국가 입장에서는 불확실성이 커짐을 뜻해, 이는 곧 한반도 문제 해결에 대해 주도권과 영향력이 약해질 수 있음을 시사한다. 이른바 한반도 문제의 ‘외재화’다. 제3부(미국과 중국 그리고 주변국들과의 관계)에서 특히 주목해볼 내용은 각 분야의 전문가들이 진단한 미중관계와 한반도의 역학관계다. 「한반도에 대한 중국의 우선순위 바꾸기」(2012)라는 유명한 보고서를 발표한 보니 글래서는 대북문제에 대한 미국과 중국의 정책 우선순위의 상이성을 진단하며, 북한의 급변사태와 관련해 미국과 중국이 정부 간 대화를 연다면 “극도로 비밀스럽고 비공개적인 대화가 될 것이며 또 그래야만 한다”라고 강조해 ‘외재화’ 문제에 대한 경각심을 일깨운다. 오바마 행정부의 내부사정을 가장 잘 아는 전문가로 꼽히는 리처드 부시는 ‘다양한 경제제재를 통해 자원 유입이 제한된다면, 북한은 자신들의 정책에 대해 재평가를 하게 될 것’이라며 대북제재를 강조했다. 또한 대북제재의 효과를 증대시키기 위해 중국의 적극적 제재 참여가 중요하다고 역설했다. 그에 이어 한국계이자 대북 강경파로 알려진 빅터 차는 북한문제의 해법으로 ‘매파적 관여’를 제안한다. 한반도문제에 이어 인터뷰의 논의는 한미일 삼각관계로 확장되는데, 지난 미 대선 당시 공화당 예비내각의 국무부 동아태 차관보 0순위 후보였던 마이클 그린은 한일관계가 미 외교정책에 끼치는 악영향에 대해 말한다. 일본의 우경화 경향이 뚜렷해진 현 상황에서 미 보수층 주류의 주장을 대변하는 소장학자 제니퍼 린드의 인터뷰는 상당한 시사점을 제시한다. 그는 전후 독일의 사례를 들어 일본이 과거 침략 전쟁에 대해 사죄할 필요가 없다고 주장했고, 이는 곧 한미일 삼각안보체제 구축을 목표로 하는 미국의 전략가들에게 유용한 논리로 수용되었다. 즉 한미일 삼각안보를 통한 중국 견제라는 목표 하에서 과거사 문제에 대한 한국인의 감정은 대수롭지 않은 것으로 취급됨을 시사한다. 이밖에도 중국과 대만 문제에 대한 미국의 관점을 진단한 조너선 폴락과 랜들 슈라이버의 분석도 동아시아 문제의 주요 분쟁 요소들에 대한 다각도의 해석을 제공해준다. 뜨는 중국이 아닌 여전한 패권국 미국의 전략에 주목하라 ‘아시아 회귀’ 전략은 앞으로도 장기적으로 미국 외교정책의 핵심이 될 가능성이 높고, 중국은 이 정책 내에서 최우선 순위를 차지할 것이다. 한반도는 미중 간 지정학적 경계선에 위치하고 있어 이 전략에 대한 이해가 반드시 필요한 상황이나 지금까지의 전문가나 언론의 분석은 미중 정상회담이나 국제 영토분쟁 등 현안에 대한 소개나 해설 수준에 그쳤고, 중국의 입장에서 미중관계를 바라보는 관심은 급속히 늘었어도 정작 여전히 패권적 우위를 지닌 미국의 입장에서 이를 바라보는 노력은 소홀했음이 사실이다. 한반도가 미중관계에 관심을 기울여야 하는 필요성은 엮은이가 선택한 역어에서부터 잘 구현되고 있다. 이 책에서는 ‘Pivot to Asia’의 ‘pivot’을 ‘회귀’로 옮겼다. ‘아시아로의 중심축 이동’이나 ‘아시아 중시’라고 번역하기도 하지만, 이 용어의 탄생 과정을 보면 오바마 대통령이나 클린턴 전 국무장관 등이 2012년 대선을 앞두고 중국을 군사적·지정학적으로 견제하고 있음을 강조하기 위해 의도적으로 사용한 측면이 강하다. 즉 ‘pivot’에는 이라크·아프가니스탄 전쟁 때 중동 지역에 집중적으로 배치되었던 군사적 자산을 미 태평양사령부로 전환·배치하고, 호주와 필리핀 등 아시아 각국과의 느슨해진 군사동맹을 다시 강화한다는 의도가 강하게 깔려 있다. ‘pivot’이 진행되면서 중국과의 군사적 대결이 언론에 의해 집중적으로 부각되고 중국의 반발이 거세지자 2012년 대선 이후 백악관은 ‘pivot’을 ‘rebalancing’으로 바꾸어 말하기 시작했다. 이 책에서는 이를 ‘재조정’으로 옮겼다. ‘rebalancing’은 외교안보 정책의 전략적 우선순위를 유럽, 중동, 아시아 간에 지역별로 재조정하고, 아시아 정책에서 외교와 군사력의 균형을 재조정한다는 보다 ‘순화된’ 뜻을 담고 있다. 결국 ‘아시아 회귀’는 미국이 동아시아에 대해 정치군사·경제·외교 측면에서 총체적·다층적으로 개입하려는 전략이라 볼 수 있다. 아시아 각국은 어떤 형태로든 그 영향권에 놓이게 될 것이고, 한반도에는 직접적 영향뿐만 아니라 우회적·간접적인 영향도 상당할 것이다. 미국의 일본에 대한 대중국 역할론이 강해질수록 일본의 재무장, 우경화 움직임이 활발해지는 것도 이에 대한 예라 할 수 있다. 한국의 외교와 정치에, 나아가 한반도 정세에 지대한 영향을 끼칠 미국의 ‘아시아 회귀’ 전략과 미중관계는 이제 우리의 생존과 연계된 문제다. Changbi Publishers
- Table of Contents:
9클래스 흑마도사, 회귀하다 5 – 윤정현 – Google Sách
- Article author: books.google.com.vn
- Reviews from users: 1220
Ratings
- Top rated: 4.4
- Lowest rated: 1
- Summary of article content: Articles about 9클래스 흑마도사, 회귀하다 5 – 윤정현 – Google Sách Updating …
- Most searched keywords: Whether you are looking for 9클래스 흑마도사, 회귀하다 5 – 윤정현 – Google Sách Updating '마왕조차 굴복시켜 스스로 마왕과 같은 존재가 된 9클래스 흑마도사 아슈란. 용사들이 그의 심장을 찔러 죽음에 이른 순간, 놀랍게도 과거로 회귀하게 되는데… 아슈란. 그의 새로운 인생의 2막이 시작된다.
- Table of Contents:
웹 브라우저 속 머신러닝 TensorFlow.js: 실전 예제로 배우는 텐서플로 머신러닝 모델 – 카이 사사키, 유수연 – Google Sách
- Article author: books.google.com.vn
- Reviews from users: 36233
Ratings
- Top rated: 3.5
- Lowest rated: 1
- Summary of article content: Articles about 웹 브라우저 속 머신러닝 TensorFlow.js: 실전 예제로 배우는 텐서플로 머신러닝 모델 – 카이 사사키, 유수연 – Google Sách Updating …
- Most searched keywords: Whether you are looking for 웹 브라우저 속 머신러닝 TensorFlow.js: 실전 예제로 배우는 텐서플로 머신러닝 모델 – 카이 사사키, 유수연 – Google Sách Updating 웹 브라우저에서 머신러닝 모델을 구축하기 위한텐서플로와 자바스크립트의 운명적 만남 TensorFlow.js는 웹에서 머신러닝 모델을 개발 및 학습시키고, 브라우저나 Node.js에 배포하는 라이브러리다. 이 책은 밑바닥부터 웹 기반 애플리케이션에 머신러닝 기술을 구현하려는 프런트엔드 웹 개발자에게 TensorFlow.js 에코시스템, 회귀, 군집화, 고속 푸리에 변환, 차원 축소 등 머신러닝 관련 기술 및 알고리즘을 다루는 방법을 친절히 설명한다. 각 장의 마지막에는 연습 문제와 더 읽을거리를 제공해 다양한 실습을 할 수 있고, 머신러닝 지식도 확장할 수 있다. 웹 환경에서 머신러닝을 바로 실행해 사용자 맞춤형 콘텐츠를 만들어보자.다양한 분야의 개발자가 쉽게 접근할 수 있는 머신러닝 이 책은 웹 개발자뿐 아니라 머신러닝, 딥러닝, 데이터 분석 종사자 등 웹에서 머신러닝 모델을 실행하려는 모든 이를 대상으로 쓰였다. 머신러닝 관련 다양한 이론을 쉽게 설명하여 이해하기도 쉽고, 머신러닝 기술을 웹에서 구축하기 위해 바로 활용할 수 있는 실전 예제를 가득 담았다. 또한, 웹에서 머신러닝 기술을 직접 실습해보며 개념을 더 쉽고, 명확하고, 탄탄하게 잡을 수도 있다. 기술 이해에 도움이 되는 많은 참고 자료와 그림, 수식을 통해 머신러닝 기술이 어떻게 프런트까지 닿게 되는지 쉽고 빠르게 이해하길 바란다. 주요 내용TensorFlow.js 설치 방법과 환경 구축 방법케라스 모델을 TensorFlow.js로 가져오는 방법TensorFlow.js 프레임워크와 라이브러리 사용법다항 회귀, 로지스틱 회귀 등 다양한 모델 사용법군집화 알고리즘과 비지도 학습법차원 축소와 t-분포 확률적 임베딩머신러닝 애플리케이션 배포 방법머신러닝 성능 향상을 위한 튜닝법과 TensorFlow.js의 전망
- Table of Contents:
회귀한 헌터는 현질로 강해진다 1권 – 쌘곰 – Google Sách
- Article author: books.google.com.vn
- Reviews from users: 7582
Ratings
- Top rated: 4.0
- Lowest rated: 1
- Summary of article content: Articles about 회귀한 헌터는 현질로 강해진다 1권 – 쌘곰 – Google Sách Updating …
- Most searched keywords: Whether you are looking for 회귀한 헌터는 현질로 강해진다 1권 – 쌘곰 – Google Sách Updating 부족한 각성능력 때문에, 자신이 얻었어야 할 정당한 몫을 뺏기고길드의 그림자로서 살아왔던 F급 헌터 김지혁.죽음의 문턱에 서고 나서야,자신에게 몰랐던 잠재력이 있었다는 걸 알았다.“내 소원은 회귀다!”소원의 돌로 헌터로 각성했던 시절로 회귀한 김지혁.이번 생은,현질로 모든 세계를 쓸어담겠다.[회귀한 헌터는 현질로 강해진다]
- Table of Contents:
See more articles in the same category here: https://toplist.maxfit.vn/blog/.
회귀 모델에서 ‘회귀’란 무엇인가?
페이스북에서 ‘regression model에서 regression 이라는 용어는 잘못되었다’ 는 글(https://www.facebook.com/dgtgrade/posts/1153483458043852) 를 봤습니다.
우선 ‘회귀(regression)’ 라는 단어가 일상에서 잘 안쓰이는 단어이고 직관적이지 못하다는 점은 저도 공감합니다. 수학이나 과학 용어 중에는 이렇게 비직관적이고 어려운 용어들이 많이 있죠. 따라서 이런 용어들을 좀 더 쉬운 단어로 바꿔야 한다고 생각합니다. 그러나 비록 회귀 모델의 ‘회귀’라는 용어가 비직관적이긴 하지만 잘못된 용어라고는 생각하지 않습니다.
이 글에서는 그 이유를 설명하기 위해 제가 이해하는 ‘회귀’의 의미와 함께 회귀 모델에 대해 정리합니다.
0. 회귀 모델이란 무엇인가?
이 글은 이미 회귀 모델이 무엇인지에 대해서 기본적인 지식은 있다는 전제하에 내용을 전개해 나가겠지만 명확한 소통을 위해 회귀 모델에 대해 다음과 같이 정의를 내리고 시작합니다.
회귀 모델은 어떤 연속형 데이터 Y와 이 Y의 원인이 되는(엄밀히 말해 원인이라고 추정되는) X간의 관계를 추정하기 위해 만든 아래와 같은 형식의 관계식을 말합니다.
Y = f(X)
그런데 실제 데이터는 측정상의 한계나 기타 여러 가지 원인으로 인해 데이터 자체에 잡음이 들어가거나 유실이 발생합니다. 따라서 실제로는 수학이나 물리학의 수식들처럼 정확한 관계식(equation function)을 만들 수 없기 때문에 다음과 같이 확률 변수인 오차항을 두게 됩니다.
Y = f(X) + e
예를 들어 온도에 따른 어떤 물질의 부피 변화에 대한 관계식을 물리학에서는 ‘부피 = w*온도’ 라고 정의할 것입니다. 그러나 실제 실험에서 온도에 따라 물체의 부피를 측정하면 정확하게 위 관계식에 맞는 w를 찾을 수 없습니다. 왜냐하면 측정상의 오차나 실험 환경 상에서 발생하는 여러 가지 변수(이를 테면 습도)들이 영향을 줄테니까요. 물리학에서는 이런 오차는 무시하고 수식을 만들지만 통계학에서는 이런 오차를 모두 e라는 확률 변수로 대신 표기합니다.
얼핏 생각하기에 여기서 중요한 것은 부피와 온도 사이의 관계이기 때문에 e 라는 오차항은 그냥 무시하면 될 것 같습니다. 그리고 실제로 만약 우리가 f(X)를 정확하게 알고 있다면 e는 무시해도 됩니다. 심지어 E=MC^2 같은 수식을 생각해 보면, 물리학에서는 관계 계수인 w의 구체적인 값도 그냥 적당히 무시해 버리는 대인배의 풍모를 자랑합니다. 그러나 데이터 분석가들은 매우 쪼잔한 존재이기 때문에 모델링을 할 때는 f(X)를 모르는 상태에서 이것을 추정하는 것부터 시작하기 때문에 이 오차항을 무시할 수 없습니다. 다시 말해 내가 추정한 회귀 모델인 f(X)를 실제 데이터에 적용했을 때 나오는 오차항이 무시해도 좋은 정도인지 먼저 확인해 본 후, 무시해도 좋다고 판단될 때만 무시해야 합니다. 그러나 대개는 이런 사실을 모르거나, 귀찮거나 아니면 이 검정을 통과할만큼 정확한 모델을 만들 방법이나 시간이 부족해서 무시하고 넘어갑니다.
여기서 오차항에 대해 이렇게 강조하는 이유는 바로 이 오차항이 회귀 모델에서 ‘회귀’의 의미를 이해하는 것과 깊은 관련이 있기 때문입니다.
1. 무엇이 어디로 ‘회귀’하는가?
회귀의 사전적 정의는 ‘한바퀴 돌아 제자리로 돌아가다’ 입니다. 따라서 회귀 모델에서 말하는 ‘회귀’의 의미를 이해하려면 무엇이 어디로 회귀하는 것인지 아는 것이 중요합니다. 위 링크 글을 비롯하여 많은 글에서는 이 회귀에 대해 골턴이 제시했던 ‘평균으로의 회귀’를 예로 들며 데이터가 회귀 모델이 제시한 추세선으로 회귀하는 것이라고 설명합니다.
그러나 위 링크의 댓글에도 나와 있듯이 데이터가 추세선으로 회귀한다는 설명은 뭔가 어색합니다. 오히려 반대로 추세선이 데이터를 따라 간다는 것이 더 맞는 설명같습니다. 그렇기 때문에 ‘regression’ 보다는 ‘progression’ 이라고 해야 한다는 주장이 나오는 것 같습니다. 그러나 제가 생각하기에 이 설명은 제대로된 설명이 아닙니다.
제가 이해하기에 회귀 모델에서 ‘회귀’는 ‘잔차(residual: 데이터의 실측치와 모델의 예측치 사이의 차이. 즉, 회귀식에서 오차항에 대한 관측치)가 평균으로 회귀하는 것’을 의미합니다. 그리고 이런 맥락에서 회귀 모델은 ‘잔차가 평균으로 회귀하도록 만든 모델’이라고 정의할 수 있습니다. 이렇게 정의를 내리고 나면 아래 문장은 부정확하다는 것을 알 수 있습니다.
‘회귀 모델링은 오차의 합이 최소가 되도록 만드는 작업이다.’
회귀 모델을 만드는 작업을 ‘데이터와의 오차합이 가장 작은 선’을 찾는 작업이라고 얘기한다면 엄밀히 말해 절반만 맞습니다. 실제 회귀 모델링을 할 때는 잔차가 최소가 되는 선을 찾기에 앞서 다음과 같은 전제 조건이 선행되어야 합니다.
데이터의 실측치와 모델의 추정치 사이의 잔차가 i.i.d.(Independent and Identically Distributed random) 성질을 만족해야 한다.
위 전제 조건을 만족하지 않으면 설령 오차가 최소가 되는 선이라 하더라도 제대로 된 회귀 모델이 아닙니다. 그 이유를 설명하려면 먼저 모델링이란 무엇인가에 대해 먼저 이해해야 합니다.
2. 모델링 = 모델의 관계식 추정 + 파라미터 추정
회귀식을 모델링할 때는 X와 Y 간의 관계에 대해 먼저 추정을 한 후 구체적인 파라미터를 추정하게 됩니다. 가령 앞부분에서 예로 든 물체의 부피와 온도에 대한 회귀식의 경우 X(온도)와 Y(부피) 사이에는 선형 관계가 있고 그 가중치가 w일 것이라는 추정을 먼저 한 것입니다. 그리고 이렇게 추정된 관계식 안에서 구체적으로 w가 무엇인지 계수에 대한 추정을 합니다.
그런데 위의 예에서 만약 실제로는 물체의 부피와 온도 사이에 아무런 관계가 없거나 혹은 온도의 제곱과 선형 관계에 있거나(부피 = w * 온도^2)아니면 온도 뿐만 아니라 습도와도 밀접하게 관련이 있다면(부피 = w1*온도 + w2*습도) 비록 오차의 합이 최소가 되도록 w를 추정하더라도 그 회귀식은 정확한 회귀 모델이 되지 못합니다. 따라서 이 회귀식을 이용해서 부피를 예측하면 실제 부피와 차이가 생길 수 밖에 없습니다.
한편, 만약 실제로 부피는 온도와 선형 관계에 있는 것이 맞다면 이 회귀 모델은 부피와 온도의 관계를 잘 추정한 모델이기 때문에 이 관계식을 이용해서 파라미터인 w를 추정하면 정확한 회귀식을 만들 수 있습니다. 그런데 설령 이렇게 정확한 모델을 만들더라도 앞서 언급했듯이 현실 세계에서의 여러 가지 오차(잡음)로 인해 이 모델을 이용해서 부피를 예측한 값과 실제 부피 사이에는 여전히 약간의 차이가 발생합니다.
결국 정확한 회귀 모델을 만들든 그렇지 못하든 항상 모델의 예측치와 실측치 사이에는 차이가 존재합니다. 다만 부정확한 회귀 모델로 인한 차이와 정확한 회귀 모델에서 발생하는 차이 사이에는 근본적으로 다른 성질이 있습니다. 즉, 정확한 모델을 만들었다면 잔차는 평균인 0으로 회귀하지만 부정확한 모델에서는 그렇지 못합니다. 이것이 위에서 얘기한 잔차의 성질입니다. 따라서 내가 추정한 관계식이 제대로 된 회귀 모델인지 여부를 판단할 때는 내가 만든 모델의 예측치와 실제값 사이의 잔차의 기대치(평균)가 0이고 평균으로 회귀하는지 살펴 봐야 합니다.
다시 말해, 내가 추정한 모델과 실제 데이터 사이의 오차가 단순히 현실 세계에 존재하는 잡음인지 아니면 내가 고려하지 못한 어떤 속성 때문인지를 알려면 잔차가 i.i.d. 한 속성을 갖고 있는지 확인해야 합니다. 이를 위해선 다음과 같은 조건을 모두 만족하는지 살펴 봐야 합니다.
잔차의 분포는 정규 분포이어야 한다.
잔차와 독립변수 X 사이에 상관 관계가 없고 자기 자신과도 상관이 없어야 한다(잔차는 독립이어야 한다).
잔차의 분포가 일정해야 한다(잔차는 등분산성을 만족해야 한다).
위 조건을 모두 만족한다면 해당 모델의 예측치와 실제 데이터 사이의 차이인 잔차는 평균으로 회귀하게 됩니다. 다시 말하면, 비록 실제 세계에서 어쩔 수 없이 존재하는 잡음으로 인해 완전히 예측치와 실측치가 일치하지는 않으며 그래서 어떤 데이터에 대해서는 그 차이가 클 수 있지만, 전체 추세로 볼 때는 잔차의 평균(대개는 0)으로 수렴합니다.
그럼 위에서 나열한 잔차의 조건에 대해서 좀 더 자세히 알아 보겠습니다.
3. 잔차의 정규성
만약 어떤 데이터에 대해 정확한 모델을 만들었다면 그 모델과 실제 데이터 사이의 오차의 확률 분포는 정규 분포를 따릅니다. 그 이유는 정규 분포 자체가 원래 오차에 대한 확률 분포이기 때문입니다. 즉, ‘왜 오차의 분포가 정규 분포를 따르는가?’ 라는 질문은 ‘왜 당근 케익에서는 당근 맛이 나는가?’ 라는 질문과 같습니다(어찌보면 통계학에서 먼저 바꿔야 할 용어는 ‘회귀’ 모델이 아니라 ‘정규’ 분포인 것 같습니다).
비록 정규 분포는 여러 수학자들에 의해서 각기 다른 방식으로 연구되었긴 하지만 이들 중에서 가장 큰 기여를 한 가우스(그래서 정규 분포를 ‘가우스의 분포’라고도 하죠)의 경우 천체 관측 시 발생하는 오차의 성질을 연구하던 중 이 정규 분포를 발견했습니다. 당시에는 기술이 발달하지 못해 천체를 눈으로 관측하다 보니 매번 관측을 할 때마다 조금씩 오차가 발생했습니다. 그런데 이런 차이값들 사이의 관계를 분석해 보니 이 값들이 평균에 근접할 수록 발생확률이 높고 평균에서 멀어질수록 확률이 떨어지는 아래와 같은 분포 규칙을 따른다는 것을 발견한 것이죠.
따라서 만약 어떤 모델이 데이터의 성질을 정확히 설명한다면 이 둘 사이의 차이는 잡음만 남게 되며 이런 잡음의 분포는 정규 분포입니다. 반대로 말해 만약 모델과 데이터 사이의 차이의 분포가 정규 분포가 아니라면 이 둘 사이의 차이에는 단순한 잡음 뿐만 아니라 내가 반영하지 못한 어떤 특징이 포함되어 있다는 것을 의미합니다.
아주 간단한 예로 다음과 같이 R에서 테스트를 해보겠습니다.
x <- 1:100 # model1 y1 <- 0.5 * x + rnorm(100)*5 m1 <- lm(y1~x) e1 <- y1 - m1$fitted.values # model2 y2 <- 0.5 * x^2 + rnorm(100)*5 m2 <- lm(y2~x) e2 <- y2 - m2$fitted.values 위에서 y1은 x와, y2는 x^2와 선형 관계를 갖는 데이터입니다. 그리고 m1은 y1 ~ x 라는 관계식으로 추정한 회귀 모델이고 m2는 y2 ~ x라는 관계식으로 추정한 회귀 모델입니다. 따라서 m1은 관계식으로 정확히 추정했지만 m2는 잘못된 회귀 모델입니다(원래는 x^2 에 대해서 모델을 추정해야 합니다). 이 상태에서 두 모델의 예측치와 실측치 사이의 잔차인 e1, e2의 히스토그램을 그려보면 아래와 같이 나옵니다. <그림 1> 두 모델의 잔차에 대한 히스토그램
이렇듯 m1의 잔차인 e1은 종모양의 분포를 띄는 반면 잘못 추정된 모델인 m2의 잔차인 e2는 왼쪽으로 쏠린 분포를 갖습니다. 이렇게 잔차의 정규 분포 여부는 히스토그램으로도 어느 정도 추정이 가능합니다. 하지만 히스토그램은 bin(막대)의 개수나 넓이를 어떻게 주느냐에 따라 모양이 크게 달라질 수 있기 때문에 다소 부정확한 자료입니다. 따라서 좀 더 정확하게 정규성 여부를 측정하고 싶다면 다른 여러 가지 방법을 사용할 수 있습니다.
이 중에서 R에서 간단하게 확인할 수 있는 방법은 아래와 같습니다.
<그림 2> Shapiro-Wilk normality test
위 방법은 Shapiro-Wilk normality test 라고 합니다. 결과로 나온 p-value가 높으면 정규 분포를 따른다고 볼 수 있으며 반대로 낮을 수록 정규 분포일 가능성이 낮습니다. 위 그림에 나와 있듯이 e1은 p-value가 0.9599 로 매우 높으며 e2는 거의 0에 가깝습니다. 따라서 이것을 통해 m2 모델의 잔차인 e2는 정규 분포를 따르지 않으며 모델이 잘못 추정되었다고 판단할 수 있습니다.
그 외에 normal quantile plot을 그려서 확인하는 방법도 있습니다. 사용 방법은 아래와 같습니다. 왼쪽 그림처럼 데이터가 qqline에서 크게 벗어나지 않으면 정규 분포를 띈다고 판단할 수 있습니다.
<그림 3> normal quantile plot
실상 데이터의 정규성을 검정하는 방법은 널리 알려진 것만해도 열 가지가 넘기 때문에 이 중에서 적절한 것을 사용하면 됩니다. 어쨌든 이렇게 잔차가 (평균이 0인) 정규 분포를 갖는다는 의미는 잔차가 평균에서 크게 벗어날 확률이 매우 낮다는 의미이며 따라서 골턴이 얘기한 ‘평균으로의 회귀’와도 연관이 깊습니다.
4. 잔차의 독립성
잔차의 분포가 정규 분포를 갖는다고 하더라도 회귀 모델을 잘 추정했다고 섣불리 판단하면 안됩니다. 더 나아가 잔차의 독립성을 확인해야 합니다. 잔차가 독립이 아니라는 말은 잔차가 어떤 패턴을 갖고 있다는 것을 의미합니다. 앞서 설명했듯이 모델을 정확히 만들었다면 잔차는 단순 잡음이기 때문에 아무런 특징을 갖고 있지 않아야 합니다. 그런데 패턴을 갖고 있다는 것은 단순 잡음이 아님을 의미하며 모델이 정확하지 않다는 뜻이 됩니다.
잔차의 독립성은 아래와 같은 두 가지 관계를 확인해야 합니다.
X와의 상관성
자기 자신과의 상관성
상관성을 확인하는 가장 쉬운 방법은 피어슨 상관 계수를 구하는 것입니다. 그러나 피어슨 상관 계수는 위 예제처럼 잔차가 x에 대해서 일정한 추세를 갖지 않고 높았다가 낮아지는 관계를 갖는다면 일정한 패턴을 갖더라도 낮은 값이 나올 수 있습니다. 따라서 이럴 때는 scatter plot을 찍어 보면 쉽게 확인이 가능합니다.
<그림 4> 잔차의 독립성 검정 – e2와 x 간에 피어슨 상관 계수는 낮게 나오지만 scatter plot을 그려보면 일정한 패턴을 갖고 있는 것을 확인할 수 있습니다.
한편, 잔차의 독립성을 검정할 때는 독립 변수인 X와의 상관성뿐만 아니라 자기 자신과의 상관성도 확인해야 합니다. 이것은 특히 시계열 데이터에서 매우 중요합니다. 시계열 분석에서 흔히 사용하는 auto regression 류의 모델은 모두 잔차의 자기 상관성을 반영한 모델입니다. 그래서 만약 독립변수와는 독립이지만 잔차가 자기 상관성을 갖는다면 이 잔차에 대한 자기 상관 관계를 모델에 반영해줘야 합니다. 예를 들어 바로 직전의 잔차와 자기 상관을 갖는 데이터라면 아래와 같이 auto regression 모델을 만들 수 있습니다.
y = f(x) + e(i)
e(i) = a1*e(i-1) + a0 + e’
물론 여기서 e(i)에 대한 잔차인 e’ 에 대해서도 동일하게 i.i.d. 성질을 만족하는지 확인해야겠죠.
이렇듯 잔차가 독립성을 가지면 데이터의 특성에 영향을 받지 않고 원래의 확률인 정규 분포를 그대로 따르게 되기 때문에 전체 추세로 볼 때 평균으로 회귀합니다. 다시 말해 ‘예측치가 데이터의 값에 영향을 받아 실측치에서 크게 벗어날 확률’이 매우 낮습니다.
5. 잔차의 등분산성
마지막으로 확인해야 할 것은 분산이 항상 일정한지 여부입니다. 아래 예를 먼저 살펴 보겠습니다.
y3 <- 0.5 * x + rnorm(100)*5 + rnorm(100)*0.2*x m3 <- lm(y3 ~ x) e3 <- y3 - m3$fitted.values plot(x, y3) abline(m3) plot(x, e3) <그림 5> 잔차의 등분산성을 만족하지 않는 예
단순히 x와 y 사이의 관계만 보면 모델을 잘 추정한 것 같지만 잔차와 x 사이의 관계를 scatter plot으로 그려 보면 x가 커질수록 잔차인 e3의 퍼짐 정도가 점점 커지는 것을 볼 수 있습니다. 반면 <그림 4>의 왼쪽 그림의 경우 e1은 x와 상관없이 퍼짐 정도가 일정합니다. 이런 경우 역시 추정한 모델이 정확한 모델이 아님을 의미합니다.
잔차의 분산이 일정치 못하다면, 특히 위 예처럼 점점 발산하는 형태를 취한다면 설령 정규 분포를 띄고 있더라도 x값이 커질수록 점점 평균에서 크게 벗어난 값을 가질 확률이 커져서 평균으로 회귀하지 못합니다. 따라서 이 모델은 실제 데이터의 성질을 잘 반영한 모델이 아닙니다.
6. 결론
잔차가 1) 정규 분포를 띄고 2) 데이터와 상관이 없으며 3) 분산이 항상 일정하다면 평균으로 회귀하는 속성을 갖습니다. 그리고 이렇게 잔차가 평균으로 ‘회귀’하도록 만든 모델을 ‘회귀 모델’이라고 합니다. 결국 회귀 모델에서 ‘회귀’ 라는 용어가 잘못되었다는 주장은 잔차의 성질을 고려하지 않은 채 회귀 모델을 이해함으로써 생긴 오해라고 생각합니다.
사실 위에서 정리한 잔차에 대한 조건은 보통 선형 회귀 모델에 대해 설명할 때 변수간의 선형 결합 관계에 대한 조건과 함께 거론됩니다. 그런데 이런 잔차의 성질은 꼭 선형 회귀 모델이 아니더라도 데이터 모델을 만들 때 염두해 둬야할 매우 중요한 정보입니다. 보통 데이터 모델의 성능을 측정할 때 R^2, RMSE, AUC 등의 값만 측정하는 경우가 많은데 보다 엄밀한 모델링을 위해선 이렇게 잔차가 어떤 특성을 갖고 있는지를 분석하는 것이 필요합니다.
회귀란??
회귀는 여러개의 독립변수와 한 개의 종속변수 간의 상관관계를 모델링하는 기법을 의미합니다.
예를들면 아파트의 방 개수, 화장실 크기 등의 독립변수에 따라서 아파트 가격인 종속변수가 어떤 관계를 가지는지를 모델링하고 예측하는 것입니다.
이를 선형 회귀식으로 표현하면 Y = W1*X1+W2*X2+W3*X2+ … , Wn*Xn 이라고 했을떼 Y는 종속변수이고 X1, X2, Xn등은 방 개수, 화장실 크기 등을 의미합니다.
W1, W2, W3, Wn은 독립변수의 영향을 미치는 회귀 계수입니다.
머신런닝 회귀 예측의 핵심은 주어진 피처와 결정 값 데이터를 통해서 최적의 회귀 계수를 찾는 것입니다.
회귀계수는 다음과 같이 나누어 집니다.
독립변수 개수 회귀 계수의 결합 1개: 단일 회귀 선형: 선형 회귀 여러 개: 다중 회귀 비선형: 비선형 회귀
지도학습은 분류와 회귀로 나누어집니다. 두개의 가장 큰 차이점은 분류는 예측값이 이산형 클래스 값이고 회귀는 연속형 숫자 값이라는 것입니다.
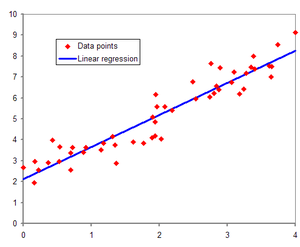
회귀 중에서는 선형 회귀가 가장 많이 사용이 됩니다. 선형 회귀는 실제 값과 예측 밧의 차이를 최소화하는 직선형 회귀선을 최적화하는 방식입니다.
선형 회귀 모델은 규제 방벙에 따라서 다시 또 유형이 나누어집니다. 규제는 선형 회귀의 과적합 문제를 해결하기 위한 방법을 말합니다. 대표적인 예시는 다음과 같습니다.
일반 선형 회귀: 예측값과 실제값의 RSS를 최소화할 수 있도록 회귀 계수를 최적화(규제를 적용하지 않은 모델)
릿지(Ridge): 릿지 회귀는 선형 회귀에 L2 규제를 추가한 회귀 모델.
라쏘(Lasso): 라쏘 회귀는 선형 회귀에 L1 규제를 적용.
엘라스틱넷(ElasticNet): L2, L1 규제를 결합한 모델. 주로 피처가 많은 데이터에 적용을 합니다.
로지스틱 회귀(Logistic Regression): 일반적으로 이진 분류뿐만이 아닌 희소 영역의 분류, 텍스트 분류와 같은 영역에서 뛰어난 예측 성능을 나타냅니다.
단순 선형 회귀
단순 선형 회귀는 독립변수도 1개, 종속변수도 1개인 선형 회귀입니다.
예시로 주택 가격이 주택의 평수로만 결정이 된다고 해봅시다. 그렇다면 다음과 같이 주택 가격은 평수에 대해서 선형의 관계로 표현할 수 있습니다.
예측값 Y’ = W0+W1*X로 계산할 수 있습니다. 독립변수가 1개인 단순 선형 회귀에서는 기울기 W1과 절편 W0을 회귀 계수로 합니다. 그리고 회귀 모델을 이런 Y’ = W0+W1*X와 같은 1차 함수로 모델링을 하면 실제 주택 가격은 이러한 1차 함수 값에서 실제 값만큼의 오류 값을 뺀(또는 더한) 값입니다.
이러한 실제 값과 회귀 모델의 차이에 따른 오류 값을 잔차라고 합니다. 최적의 회귀는 이 잔차합이 최소가 되도록 하는 것입니다.
오류 값은 +, – 가 될 수 있습니다. 그렇기 때문에 전체 데이터의 오류의 합을 구하기 위해서는 단순히 더하면 안됩니다. 그래서 계산을 할때 절댓값을 취해서 더하거나(Mean Absolute Error), 오류 값의 제곱을 구해서 더하기(RSS)를 사용합니다. 보통 미분의 계산을 편리하게 하기 위해서 RSS를 사용합니다.
회귀에서 RSS는 비용(Cost)를 의미합니다. 머신러닝 회귀 알고리즘에서는 데이터를 계속 학습하면서 이 함수가 반환하는 값을 지속해서 감소시키면서 최종적으로는 더 이상 감소하지 않는 최소의 오류 값을 구하는 것입니다. 이 비용 함수는 손실 함수(loss function)이라고도 합니다.
경사 하강법(Gradient Descent)
경사 하강법은 점진적으로 반복적인 계산을 통해서 W 파라미터 값을 업데이트 해가면서 오류 값이 최소가 되는 W 파라미터를 구하는 방식입니다.
경사 하강법은 반복적으로 비용 함수의 반환 값, 다시말해 예측값과 실제값의 차이가 작아지는 방향성을 가지고 W 파라미터를 지속해서 보정해 나갑니다. 예를 들어 최초의 오류 값이 100이라고 하면 두번째 오류값은 90, 세번째는 80과 같은 방향으로 지속해서 나아가는 것입니다. 그리고 오류 값이 더이상 작아지지 않으면 그 오류 값응ㄹ 최소 비용으로 판단하고 그때의 W 값을 최적 파라미터로 반환하게 됩니다.
Reference
파이썬 머신러닝 완벽가이드
회귀(regression)란 무엇인가?
머신러닝을 하다보니 회귀(regression)이라는 말이 나옵니다.
그런데 회귀를 잘 설명하지 않고 회귀 모델은 어쩌고 하면서 설명을 하기 때문에, 회귀에 대한 개념이 부족합니다.
회귀에 대한 설명을 찾아보면
선현 회귀는 종속 변수 y 와 한 개 이상의 독립 변수 x와의 선형 상관 관계를 모델링하는 회귀분석 기법이다. 한 개의 설명 변수에 기반하는 경우는 단순 선형 회귀, 둘 이상의 설명 변수에 기반한 경우에는 다중 선형 회귀라고 한다.
라고 합니다. 어렵게 말해놨는데, 얘를 쉽게 말하면 뭐라고 할까요?
간단하게 말하면 데이터가 어떤 데이터가 어떠한 함수로부터 생성되어있는가를 알아보는 것입니다.
다시 말하면 변수 사이의 관계를 알아보는 방법입니다.
예를 들면 어느 정도의 오차를 고려하더라도, 아버지의 키를 보고 아들의 키를 추측할 수 있지 않을까요?
부모의 키 x와 아들의 키 y가 y=a+bxy=a+x 같이 생긴 관계를 가진다면, x나 y값 중 하나만 보고 다른 것을 추측하는 방법입니다.
이렇게 쉽게 회귀에 대해 알아봤습니다.
참고
[1] – https://blog.martinwork.co.kr/ai/2018/07/10/what-is-linear-regression.html [2] – https://freshrimpsushi.tistory.com/548
So you have finished reading the 회귀 란 topic article, if you find this article useful, please share it. Thank you very much. See more: 회귀하다 뜻, 선형 회귀란, 회귀 한자, 회귀모델이란, 회귀물 뜻, 회귀분석 뜻, 머신러닝 회귀란, 딥러닝 회귀 란
