Top 44 고주파 필터 Top 8 Best Answers

You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 고주파 필터 on Google, you do not find the information you need! Here are the best content compiled and compiled by the Toplist.maxfit.vn team, along with other related topics such as: 고주파 필터 High pass filter, 저주파 필터, High pass filter 공식, High Pass Filter 원리, Low Pass Filter, 밴드패스필터, 고역통과필터, 저역통과필터

고주파, 저주파 필터, RFID

하이패스 필터 – 위키백과, 우리 모두의 백과사전

Article author: ko.wikipedia.org
Reviews from users: 21476 Ratings
Top rated: 4.4
Lowest rated: 1
Summary of article content: Articles about 하이패스 필터 – 위키백과, 우리 모두의 백과사전 하이패스 필터(High-pass filter, HPF) 또는 고주파 통과 필터는 특정한 차단 주파수 이하 주파수의 신호를 감쇠시켜 차단 주파수 이상의 주파수 신호만 통과시키는 … …
Most searched keywords: Whether you are looking for 하이패스 필터 – 위키백과, 우리 모두의 백과사전 하이패스 필터(High-pass filter, HPF) 또는 고주파 통과 필터는 특정한 차단 주파수 이하 주파수의 신호를 감쇠시켜 차단 주파수 이상의 주파수 신호만 통과시키는 …
Table of Contents:

1차 연속시간 회로[편집]

이산 시간 해석[편집]

같이 보기[편집]

각주[편집]

외부 링크[편집]

하이패스 필터 - 위키백과, 우리 모두의 백과사전 — 하이패스 필터 – 위키백과, 우리 모두의 백과사전

Article author: m.blog.naver.com
Reviews from users: 33192 Ratings
Top rated: 3.6
Lowest rated: 1
Summary of article content: Articles about 고주파필터와 저주파필터의 음양순환 : 네이버 블로그 고주파 필터를 high pass filter, 저주파 필터를 Low pass filter라고 하는데, 이는 다양한 주파수를 가진 전류 중에서 어떤 주파수를 통과시키고 … …
Most searched keywords: Whether you are looking for 고주파필터와 저주파필터의 음양순환 : 네이버 블로그 고주파 필터를 high pass filter, 저주파 필터를 Low pass filter라고 하는데, 이는 다양한 주파수를 가진 전류 중에서 어떤 주파수를 통과시키고 …
Table of Contents:

카테고리 이동

한국순환학회 인아랑 순환법칙 사상물리학화학

이 블로그
순환법칙
카테고리 글

카테고리

이 블로그
순환법칙
카테고리 글

Article author: ddangeun.tistory.com
Reviews from users: 855 Ratings
Top rated: 3.3
Lowest rated: 1
Summary of article content: Articles about 1차 Low-Pass Filter(저주파 통과필터), High-Pass Filter(고주파 통과 필터) 구현하기, 코드 저주파 통과필터(Low-Pass Filter), 고주파 통과필터 (High-Pass Filter)를 이하 lpf, hpf라 부르겠습니다. 신호 처리를 함에 있어 원하는 신호를 … …
Most searched keywords: Whether you are looking for 1차 Low-Pass Filter(저주파 통과필터), High-Pass Filter(고주파 통과 필터) 구현하기, 코드 저주파 통과필터(Low-Pass Filter), 고주파 통과필터 (High-Pass Filter)를 이하 lpf, hpf라 부르겠습니다. 신호 처리를 함에 있어 원하는 신호를 … 저주파 통과필터(Low-Pass Filter), 고주파 통과필터 (High-Pass Filter)를 이하 lpf, hpf라 부르겠습니다. 신호 처리를 함에 있어 원하는 신호를 뽑아내기 위해 lpf와 hpf를 사용하여 지지고 볶았습니다. 어느정..
Table of Contents:

‘공통 이론’ Related Articles

공지사항

최근 포스트

검색

전체 방문자

티스토리툴바

1차 Low-Pass Filter(저주파 통과필터), High-Pass Filter(고주파 통과 필터) 구현하기, 코드

Article author: dongseo.ac.kr
Reviews from users: 48619 Ratings
Top rated: 3.8
Lowest rated: 1
Summary of article content: Articles about 1차 Low-Pass Filter(저주파 통과필터), High-Pass Filter(고주파 통과 필터) 구현하기, 코드 고주파 통과 필터 영상은 저주파 통과 필터를 이용하여 얻을 수 있음. 원본 영상에서 저주파 통과 필터링으로 얻은 영상 뺀 차 영상은 고주파. 성분만 남게 됨. f. …
Most searched keywords: Whether you are looking for 1차 Low-Pass Filter(저주파 통과필터), High-Pass Filter(고주파 통과 필터) 구현하기, 코드 고주파 통과 필터 영상은 저주파 통과 필터를 이용하여 얻을 수 있음. 원본 영상에서 저주파 통과 필터링으로 얻은 영상 뺀 차 영상은 고주파. 성분만 남게 됨. f. 저주파 통과필터(Low-Pass Filter), 고주파 통과필터 (High-Pass Filter)를 이하 lpf, hpf라 부르겠습니다. 신호 처리를 함에 있어 원하는 신호를 뽑아내기 위해 lpf와 hpf를 사용하여 지지고 볶았습니다. 어느정..
Table of Contents:

‘공통 이론’ Related Articles

공지사항

최근 포스트

검색

전체 방문자

티스토리툴바

Article author: patents.google.com
Reviews from users: 1412 Ratings
Top rated: 3.1
Lowest rated: 1
Summary of article content: Articles about KR100867850B1 – ê³ ì£¼í íí° ë° ê·¸ ì ì¡°ë°©ë²
– Google Patents 본 발명은 LTCC 적층 세라믹 기판을 이용하여 공동 공진기 구조를 갖는 필터를 구현하여 대역 특성을 향상시킬 수 있는 고주파 필터 및 그 제조방법을 개시한다. …
Most searched keywords: Whether you are looking for KR100867850B1 – ê³ ì£¼í íí° ë° ê·¸ ì ì¡°ë°©ë²
– Google Patents 본 발명은 LTCC 적층 세라믹 기판을 이용하여 공동 공진기 구조를 갖는 필터를 구현하여 대역 특성을 향상시킬 수 있는 고주파 필터 및 그 제조방법을 개시한다.
ë³¸ ë°ëªì LTCC ì ì¸µ ì¸ë¼ë¯¹ ê¸°íì ì´ì©íì¬ ê³µë ê³µì§ê¸° êµ¬ì¡°ë¥¼ ê°ë íí°ë¥¼ êµ¬ííì¬ ëì í¹ì±ì í¥ììí¬ ì ìë ê³ ì£¼í íí° ë° ê·¸ ì ì¡°ë°©ë²ì ê°ìíë¤. ê°ìë ë³¸ ë°ëªì ì¸ë¼ë¯¹ ê¸°íì ì¬ì´ìëê³ ìíë¶ì ë°°ì¹ë ì 1 ëì íê³¼ ì 2 ëì í; ìê¸° ì¸ë¼ë¯¹ ê¸°í, ì 1 ëì í ë° ì 2 ëì íì´ í©ì°©ë ê°ì¥ìë¦¬ ëë ë¥¼ ë°ë¼ ë°°ì¹ëì´ ìë ë¤ìê°ì ê¸ìë°; ìê¸° ì 1 ëì íì ìë¶ì ë°°ì¹ëì´ ìë í¬í¸í; ë° ìê¸° í¬í¸í ìì ì í¸ ì¡ìì ë¨ì ìí ì íëë¡ ë°°ì¹ëì´ ìë ì 1 í¬í¸ì ì 2 í¬í¸ë¥¼ í¬í¨íë ê²ì í¹ì§ì¼ë¡ íë¤.
ì¬ê¸°ì, ìê¸° ë¤ìê°ì ê¸ìë°ë ì¬ì©íë ì£¼íì ì í¸ì íì¥ì ë°ë¼ ìê¸° ì¸ë¼ë¯¹ ê¸°íì ê°ì¥ìë¦¬ ëë ë¥¼ ì¼ì í ê°ê²©ì¼ë¡ ë¤ìê° ë°°ì¹ëì´ ìê³ , ìê¸° ê¸ìë°ì ê°ê²©ì ì£¼íì ì í¸ì íì¥ì ëíì¬ 1/50~1/100ì ëì´ë©°, ìê¸° ì¸ë¼ë¯¹ ê¸°íì í¬ê¸°ë¥¼ ì¡°ì íì¬ ë¤ìí ì£¼íì ëìì ì í¸ë¥¼ íí°ë§í ì ìë ê²ì í¹ì§ì¼ë¡ íë¤.

ê³ ì£¼í, íí°, ê¸ìë°, ê³µì§ê¸°, LTCC
Table of Contents:

Info

Links

Images

Classifications

Abstract

Description

Claims (7)

Priority Applications (1)

Applications Claiming Priority (1)

Publications (2)

ID=37319784

Family Applications (1)

Country Status (1)

Cited By (1)

Families Citing this family (2)

Citations (4)

Patent Citations (4)

Cited By (1)

Also Published As

위키백과, 우리 모두의 백과사전

하이패스 필터(High-pass filter, HPF) 또는 고주파 통과 필터는 특정한 차단 주파수 이하 주파수의 신호를 감쇠시켜 차단 주파수 이상의 주파수 신호만 통과시키는 필터를 의미한다.[1] 필터의 세부적인 주파수 응답은 필터 설계에 따라 달라진다. 고주파 통과 필터는 대개 선형 시불변 시스템으로 모델링된다. 이러한 고주파 통과 필터는 종종 오디오 부문에서 저주파 차단 필터(low-cut filter)나 저역 차단 필터(bass-cut filter)라고 부른다.[2] 고주파 통과 필터는 0이 아닌 평균 전압에 민감한 회로나 무선 주파수 장치 같은 곳에서 직류 전압을 차단하는 데 사용하는 등 다양한 분야에 활용된다. 또한 로우패스 필터와 같이 사용하여 대역 필터를 만들 수도 있다.[3]
광학에서는 “하이 패스”(High-pass)와 “로우 패스”(Low-pass)가 주파수와 빛의 파장 중 어느 쪽에 속하느냐에 따라서 서로 다른 의미를 가질 수 있다. 주파수의 하이 패스 필터(고주파 통과 필터)는 파장의 로우 패스 필터가 되며, 반대로 주파수의 로우 패스 필터(저주파 통과 필터)는 파장의 하이 패스 필터가 될 수 있다. 이 때문에 광학에서 파장 필터는 혼란을 막기 위해 로우 패스/하이 패스 대신 롱 패스(Long-pass), 숏 패스(Short-pass)라고 부른다.[4]
1차 연속시간 회로 [ 편집 ]
수동 아날로그 1차 하이패스 필터를 RC 회로 로 구현한 모습.

오른쪽 그림과 같은 간단한 1차 하이패스 필터 회로는 입력 전압에 저항기와 축전기를 직렬로 이어 달고 저항기의 전압을 출력 전압으로 만들어 구현한다. 이 선형 시불변 시스템의 전달 함수는 다음과 같다.

V o u t ( s ) V i n ( s ) = s R C 1 + s R C . {\displaystyle {\frac {V_{\rm {out}}(s)}{V_{\rm {in}}(s)}}={\frac {sRC}{1+sRC}}.}

여기서 저항과 캐패시턴스(정전 용량)의 곱(R×C)이 시간 상수(τ)이며 이는 차단 주파수 f c 와 반비레한다. 즉 아래의 식이 성립한다.

f c = 1 2 π τ = 1 2 π R C , {\displaystyle f_{c}={\frac {1}{2\pi \tau }}={\frac {1}{2\pi RC}},\,}

여기서 차단 주파수란 필터의 극점이 필터의 주파수 응답을 벗어나는 시점의 주파수이다. 이보다 낮은 주파수일 경우 그 주파수의 신호는 차단당한다. 위 식을 통해 라플라스 변환 주파수 응답인 H ( s ) = V o u t ( s ) V i n ( s ) {\displaystyle H(s)={V_{\rm {out}}(s) \over V_{\rm {in}}(s)}} 을 그리면 아래와 같다.

H ( s ) = V o u t ( s ) V i n ( s ) = s ω 0 ( 1 + s ω 0 ) {\displaystyle H(s)={V_{\rm {out}}(s) \over V_{\rm {in}}(s)}={s\omega _{0} \over (1+s\omega _{0})}}

능동 하이패스 필터

오른쪽의 능동 하이패스 필터는 연산 증폭기를 사용한 1차 하이패스 필터이다. 여기서의 선형 시불변 시스템 전달 함수는 아래와 같다.

V o u t ( s ) V i n ( s ) = − s R 2 C 1 + s R 1 C . {\displaystyle {\frac {V_{\rm {out}}(s)}{V_{\rm {in}}(s)}}={\frac {-sR_{2}C}{1+sR_{1}C}}.}

여기서 필터는 통과 대역에서 -R 2 /R 1 의 이득을 가지며 차단 주파수는

f c = 1 2 π τ = 1 2 π R 1 C , {\displaystyle f_{c}={\frac {1}{2\pi \tau }}={\frac {1}{2\pi R_{1}C}},\,}

다음과 같다.

이 회로는 능동 회로이므로 필터의 이득이 상수형이 아닐 수 있다. 이 경우 고주파 신호가 반전되고 R 2 /R 1 만큼 증폭될 수 있다.

이산 시간 해석 [ 편집 ]
이산 시간에서의 하이패스 필터도 생각할 수 있다. 연속 시간 하이패스 필터를 이산 시간으로 샘플링하면 연속시간의 동작을 이산화할 수 있다.

우선, 위 문단에서의 RC 회로에서의 주파수 응답에 키르히호프의 전기회로 법칙과 전기용량를 이용하면 아래와 같다.

{ V out ( t ) = I ( t ) R (V) Q c ( t ) = C ( V in ( t ) − V out ( t ) ) (Q) I ( t ) = d ⁡ Q c d ⁡ t (I) {\displaystyle {\begin{cases}V_{\text{out}}(t)=I(t)\,R&{\text{(V)}}\\Q_{c}(t)=C\,\left(V_{\text{in}}(t)-V_{\text{out}}(t)\right)&{\text{(Q)}}\\I(t)={\frac {\operatorname {d} Q_{c}}{\operatorname {d} t}}&{\text{(I)}}\end{cases}}}

여기서 Q c ( t ) {\displaystyle Q_{c}(t)} 는 t {\displaystyle t} 시간에 축전지에 충전되어 있는 전하량을 의미한다. 위 식에서 (Q) 식을 (I) 식에, (I) 식을 (V) 식에 대입하여 정리하면 아래와 같다.

V out ( t ) = C ( d ⁡ V in d ⁡ t − d ⁡ V out d ⁡ t ) ⏞ I ( t ) R = R C ( d ⁡ V in d ⁡ t − d ⁡ V out d ⁡ t ) {\displaystyle V_{\text{out}}(t)=\overbrace {C\,\left({\frac {\operatorname {d} V_{\text{in}}}{\operatorname {d} t}}-{\frac {\operatorname {d} V_{\text{out}}}{\operatorname {d} t}}\right)} ^{I(t)}\,R=RC\,\left({\frac {\operatorname {d} V_{\text{in}}}{\operatorname {d} t}}-{\frac {\operatorname {d} V_{\text{out}}}{\operatorname {d} t}}\right)}

위 방정식을 이산화시킬 수 있다. 식을 단순하게 풀기 위해 입력 신호와 출력 신호를 일정한 시간 간격인 Δ T {\displaystyle \Delta _{T}} 마다 샘플링된다고 가정하여 보자. 여기서 샘플링 된 입력 신호 V in {\displaystyle V_{\text{in}}} 는 ( x 1 , x 2 , … , x n ) {\displaystyle (x_{1},x_{2},\ldots ,x_{n})} 마다 값이 존재하며 출력 신호 V out {\displaystyle V_{\text{out}}} 는 V out {\displaystyle V_{\text{out}}} 마다 존재하게 샘플링되어 있다. 이를 하나로 묶으면 다음과 같다.

y i = R C ( x i − x i − 1 Δ T − y i − y i − 1 Δ T ) {\displaystyle y_{i}=RC\,\left({\frac {x_{i}-x_{i-1}}{\Delta _{T}}}-{\frac {y_{i}-y_{i-1}}{\Delta _{T}}}\right)}

이 식을 점화식 형태로 만들면 다음과 같다.

y i = R C R C + Δ T y i − 1 ⏞ Decaying contribution from prior inputs + R C R C + Δ T ( x i − x i − 1 ) ⏞ Contribution from change in input {\displaystyle y_{i}=\overbrace {{\frac {RC}{RC+\Delta _{T}}}y_{i-1}} ^{\text{Decaying contribution from prior inputs}}+\overbrace {{\frac {RC}{RC+\Delta _{T}}}\left(x_{i}-x_{i-1}\right)} ^{\text{Contribution from change in input}}}

여기서 1차 연속시간 RC 필터의 이산 시간 구현은 다음으로 적을 수 있다.

y i = α y i − 1 + α ( x i − x i − 1 ) where α ≜ R C R C + Δ T {\displaystyle y_{i}=\alpha y_{i-1}+\alpha (x_{i}-x_{i-1})\qquad {\text{where}}\qquad \alpha \triangleq {\frac {RC}{RC+\Delta _{T}}}}

위에서의 정의에 따라 0 ≤ α ≤ 1 {\displaystyle 0\leq \alpha \leq 1} 이다. 여기서 변수 α {\displaystyle \alpha } 를 샘플링 간격 Δ T {\displaystyle \Delta _{T}} 와의 곱을 통해 시간 상수 R C {\displaystyle RC} 로 만들 수 있다.

R C = Δ T ( α 1 − α ) {\displaystyle RC=\Delta _{T}\left({\frac {\alpha }{1-\alpha }}\right)}

여기서

f c = 1 2 π R C {\displaystyle f_{c}={\frac {1}{2\pi RC}}} R C = 1 2 π f c {\displaystyle RC={\frac {1}{2\pi f_{c}}}}

이므로 α {\displaystyle \alpha } 와 f c {\displaystyle f_{c}} 에는 다음과 같은 관계를 이루게 된다.

α = 1 2 π Δ T f c + 1 {\displaystyle \alpha ={\frac {1}{2\pi \Delta _{T}f_{c}+1}}} f c = 1 − α 2 π α Δ T {\displaystyle f_{c}={\frac {1-\alpha }{2\pi \alpha \Delta _{T}}}}

같이 보기 [ 편집 ]
각주 [ 편집 ]
외부 링크 [ 편집 ]

고주파필터와 저주파필터의 음양순환

RL회로에서 직류일때는 저항 효과가 없어서 전류가 잘 흐릅니다. 반면 RC회로에서 직류일때는 저항 때문에 전류가 흐르지 않습니다.

⊙ 직류일때 RL회로는 코일(L)에 저항이 0이므로 전류가 잘 흐름

⊙ 직류일때 RC회로는 축전기(C)가 충전되면서 전하이동이 차단되어 전류가 안 흐름

하지만 교류일때는 전류의 세기와 방향이 변화하므로, 코일에서는 유도기전력에 의한 저항효과가 발생하고, 축전기에서는 충전과 방전에 의한 저항효과가 발생하는데, 이를 리액턴스라고 합니다. 따라서 교류일때는 직류일때보다 전류의 세기가 약해집니다.

LC 또는 RLC 회로에서

⊙ 리액턴스 : 코일(L) 또는 축전기(C)에서 발생하는 저항

⊙ 임피던스 : 저항(R)과 리액턴스가 합성된 저항

교류에서의 코일의 저항을 유도리액턴스(XL)라고 하며, 주파수(f)와 유도계수(L)에 비례합니다.

교류에서의 축전기의 저항을 용량리액턴스(Xc)라고 하며, 주파수(f)와 전기용량(C)에 반비례합니다.

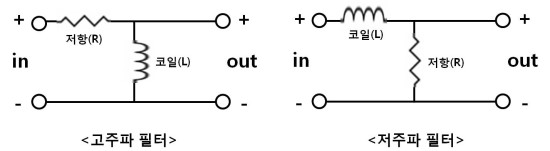
코일과 축전기는 반대작용을 하는데, 이를 각각 활용하면 코일을 사용하는 고주파필터(높은 주파수 통과), 저주파필터(낮은 주파수 통과)와 축전기를 사용하는 고주파필터(높은 주파수 통과), 저주파필터(낮은 주파수 통과)를 만들 수 있습니다.

고주파 필터를 high pass filter, 저주파 필터를 Low pass filter라고 하는데, 이는 다양한 주파수를 가진 전류 중에서 어떤 주파수를 통과시키고 차단시킬 것인가의 개념입니다. 저항과 코일을 통해서 주파수 대역을 조절할 수 있습니다.

코일이나 축전기나 둘다 저항 역할을 하나, 교류의 주파수가 클수록 코일의 저항효과가 크고, 주파수가 작을수록 축전기의 저항효과가 커집니다.

out에는 스피커와 같은 전기기구가 연결되는데, 왼쪽처럼 코일(L)이 전기기구와 병렬로 연결되고 저항(R)과는 직렬로 연결될때, 교류회로의 주파수가 커질수록 코일에 저항이 커지게되고, 코일과 전기기구에는 큰 전압이 걸리면서 전기기구에 전류가 잘흐르게 됩니다. 오른쪽처럼 코일(L)이 전기기구와 직렬로 연결되고 저항(R)과는 병렬로 연결될때, 교류회로의 주파수가 작아질수록 코일의 저항이 작아지게되고, 저항과 전기기구에는 큰 전압이 걸리면서 전기기구에 전류가 잘 흐르게 됩니다.

축전기(C)의 경우 왼쪽처럼 전기기구와 직렬로 연결되고 저항(R)과 병렬로 연결될때, 교류회로의 주파수가 커질수록 축전기에 저항이 작아지게되고, 저항과 전기기구에는 큰 전압이 걸리면서 전기기구에 전류가 잘 흐르게 됩니다. 오른쪽처럼 축전기(C)가 전기기구와 병렬로 연결되고 저항(R)과는 직렬로 연결될때, 교류회로의 주파수가 작아질수록 축전기의 저항이 작아지게되고, 축전기와 전기기구에 큰 전압이 걸리면서 전기기구에 전류가 잘 흐르게 됩니다.

결국 교류에서는 코일의 경우 병렬로 연결됐을때 주파수가 클수록 코일에 저항이 커져 전기기구에 전압이 커지면서 전기기구에 전류가 잘 흐릅니다. 축전기의 경우 직렬로 연결됐을때 주파수가 클수록 축전기에 저항이 작아져 전기기구에 전압이 커지면서 전기기구에 전류가 잘흐릅니다.

밴드 패스 필터(band pass filter)는 특정 주파수 이상과 이하의 주파수를 제거하고 출력하는 필터입니다. 위의 그림은 축전기를 사용하였는데, 반대로 코일을 역으로 사용하여도 마찬가지 효과를 냅니다. 위의 그림의 중앙을 기준으로 왼쪽은 저주파필터, 오른쪽은 고주파필터로 작용합니다. 밴드 리젝트 필터(band reject filter)는 밴드 패스 필터와는 반대로 특정 주파수 사이의 주파수는 차단하고 그이상과 그이하의 주파수만을 통과시키는 필터입니다.

<참고문헌과 관련자료 : RLC Circuits and Filters - Dr. stienecker's>

LC회로는 저항(R)없이 코일(L)과 축전기(C)를 연결한 것이고, RLC회로는 저항(R)이 포함된 것입니다. LC회로와 RLC회로의 차이점은 LC회로는 저항이 없기 때문에 전류의 손실없이 진동하는 전기진동을 만들 수 있는 이상적인 회로입니다. 하지만 레이더, 라디오, 무선기기 등을 만들려면 전기기구가 필요하게 되고, 결국 전기기구는 저항(R)과 같은 역할을 합니다. 따라서 RLC회로는 전류의 소모가 있습니다. 전기기구가 없더라도 저항(R)에서 열이 발생하게 됩니다.

RL회로, RC회로 뿐만아니라, RLC회로를 이용해서도 주파수의 대역폭을 조절할 수 있습니다. 이 RLC 회로에는 많은 응용 프로그램이 있습니다. 다양한 유형의 발진기 회로에 사용되며, 라디오 수신기 또는 텔레비전 세트와 같이 주변 전파에서 좁은 범위의 주파수를 선택하여 사용되는 튜닝의 목적이 있습니다. RLC 회로는 대역 통과 필터, 대역 정지 필터, 저주파 통과 필터, 고주파 통과 필터로 사용할 수 있습니다.

<밴드 패스 필터의 대역>

<그림출처 : Low-pass filter - 위키백과, 대역필터 - 위키백과, RLC circuit - 위키백과>

위의 그림에서 f0은 중심주파수이고 B는 대역폭입니다. FL은 저주파차단주파수 FH은 고주파차단주파수를 나타냅니다. 중심주파수에서는 신호의 손실이 없지만, 중심주파수에서 좌와 우로 멀어질때 완만하게 감쇠가 발생하므로, 3dB 대역폭은 신호 진폭이 3dB씩 감소하는 주파수로, 일반적으로 대역 통과 필터의 대역폭은 보통 3dB 대역폭으로 정의됩니다. 밴드 패스 필터는 원하지 않는 신호를 차단하는데 사용하므로, 다른 신호를 차단하면서 최소한의 손실만으로 통과할 수 있도록 설계됩니다. 하지만 밴드 패스 필터가 날카롭게 특정 주파수를 차단할 수 없으므로 대역 통과 필터의 대역폭은 최소 감쇠로 통과할 수 있는 주파수 범위입니다. 신호의 전력이 최대값에서 3dB 감소하는 주파수를 3dB 대역폭이라고 하며, 이것은 신호 전력이 최대값의 절반이 되는 지점이기도 합니다. 이러한 3dB 대역폭은 중심 주파수의 최대값이 피크에서 0.707까지 감쇠되는 양의 주파수 범위이기도 합니다. 따라서 밴드패스필터 대역은 amplitude drop은 70.7%이고(전압 이득), power drop((0.707)2 = 0.5)는 50%(전력 이득)인 대역폭(위의 그림에서 B)이 됩니다. -3dB 대역폭은 진폭 변화가 양쪽으로 0.707인 주파수 범위를 나타내며, 이것은 출력이 0.5인 범위에 해당합니다. 이를 데시벨(dB)로 환산하면 0.5의 출력비는 ≥-3dB과 같습니다.

코일(L)과 축전기(C)는 서로 반대 역할을 하므로 RL회로, RC회로처럼 이를 응용하여 고주파 또는 저주파 필터로 이용할 수 있습니다. 특히 RLC회로는 전기진동을 하는 필터가 됩니다.

따라서 RL회로, RC회로는 스피커의 주파수 용도(고음용, 저음용)로, RLC회로는 라디오의 주파수 용도(주파수 튜닝)로 주로 사용됩니다.

<관련자료>

1차 Low-Pass Filter(저주파 통과필터), High-Pass Filter(고주파 통과 필터) 구현하기, 코드

728×90

반응형

저주파 통과필터(Low-Pass Filter), 고주파 통과필터 (High-Pass Filter)를 이하 lpf, hpf라 부르겠습니다.

신호 처리를 함에 있어 원하는 신호를 뽑아내기 위해 lpf와 hpf를 사용하여 지지고 볶았습니다.

어느정도 원리를 깨달았죠.. 코드만 원하시면 밑으로 가면 됩니다. ㅎㅎ

<칼만필터는 어렵지 않아> 책을 참고하였습니다.

1차 Low-Pass Filter

lpf는 말그대로 신호의 낮은 주파수 부분을 통과시키는 건데요, 즉 신호의 높은 주파수(예를 들어 진동이나 노이즈)를 없애 신호를 좀더 매끄럽게 만들어 줍니다. 그러므로 자주 사용되죠.

이런식으로 효과를 볼 수 있습니다.

Smoothing이라고도 하죠. 그냥 lpf입니다.

단순히 생각하면 lpf를 만들기 위해선 이전 측정값과 현재 측정값에 가중치를 두어 계산하면 됩니다.

다시말하면, 이전 값을 고려하여 현재값을 정하고, 이전값에 어느정도 비중을 둔 현재값을 계산하면 됩니다.

α는 1에서 0사이의 값이고, x_k는 k번째 측정값, x바는 계산된 값(추정값, lpf 필터된 값)입니다.

α가 클수록 이전 값에 비중이 커져 더 그래프가 부드러워지고, 잡음이 줄어듭니다. 하지만 반대로 실제 값과는 달라지게 되겠죠.

하지만 시간 영역에서 α를 설계하기는 쉽지 않습니다. 보통 차단주파수를 정해 lpf를 사용하는데, 이를 위해 시간영역의 식을 주파수 영역의 식으로 바꾸어 주면 됩니다.

이는 라플라스 변환 식을 사용하면 됩니다.

위의 식이 라플라스 변환 식입니다. 간단히 대입만 해주면 됩니다.

lpf의 시간영역식과 라플라스 변환한 주파수 영역의 식은 다음과 같이 나타낼 수 있습니다.

여기서 G(s)는 output/iniput의 형태로 나타내고, 전달함수라고 부릅니다.

간단한 lpf 필터 전달함수는 다음과 같이 나타낼 수 있습니다.

이 식은 1차 lpf 회로에서 나왔습니다.

키르히호프 전압법칙에 의해 미분방정식이 나옵니다.

주파수 영역으로 바꾸어줍니다.

전달함수를 구합니다.

또한 전달함수의 s(주파수)가 0이나 무한대로 갈때 어디로 수렴하는지 보면 lpf인지, hpf인지 알 수 있습니다.

낮은 주파수를 통과하는 저주파 통과 필터인 것을 알 수 있습니다.

위의 전달 함수를 다시 다음과 같이 써줍니다.

위의 식을 라플라스 역변환 합니다. s가 곱해지면 미분함수가 되므로, 다음과 같이 쓸 수 있습니다.

이산 신호인것을 고려하여 다음과 같이 바꾸어 줍니다.

위와 같이 1차 lpf 식을 만들 수 있습니다.

// lowpass filter float lpf(float x_k, float y_km1, float Ts, float tau) { float y_k; y_k = (tau * y_km1 + Ts * x_k) / (Ts + tau); return y_k; }

위 식을 보면, 알파는 다음과 같음을 알 수 있습니다.

τ(tau)는 다음과 같이 정해집니다.

w_cut은차단 각주파수(rad/s), f_cut은 차단주파수(Hz)입니다.

1차 High-Pass Filter

hpf는 신호의 변화만 캐치하는데 효과적입니다.

예를들어 적분시 발생하는 적분 상수를 제거한다던지, 0Hz의 전압이나 offset 등을 제거하는데 사용하곤 했습니다.

lpf처럼 hpf도 다음과 같이 전달함수를 쓸 수 있습니다.

높은 주파수의 신호만 통과하는 것을 확인할 수 있습니다.

이제 라플라스 역변환후, 이산신호의 식으로 바꾸어 줍니다.

// highpass filter float hpf(float x_k, float x_km1, float y_km1, float Ts, float tau) { float y_k; y_k = (tau/(tau + Ts) * y_km1) + (tau/(tau + Ts)) * (x_k – x_km1); return y_k; }

끝!^^

728×90

반응형

So you have finished reading the 고주파 필터 topic article, if you find this article useful, please share it. Thank you very much. See more: High pass filter, 저주파 필터, High pass filter 공식, High Pass Filter 원리, Low Pass Filter, 밴드패스필터, 고역통과필터, 저역통과필터

Top 44 고주파 필터 Top 8 Best Answers

하이패스 필터 – 위키백과, 우리 모두의 백과사전

고주파필터와 저주파필터의 음양순환 : 네이버 블로그

1차 Low-Pass Filter(저주파 통과필터), High-Pass Filter(고주파 통과 필터) 구현하기, 코드

1차 Low-Pass Filter(저주파 통과필터), High-Pass Filter(고주파 통과 필터) 구현하기, 코드

KR100867850B1 – ê³ ì£¼í íí° ë° ê·¸ ì ì¡°ë°©ë²
– Google Patents

RF È¸·Î°³³ä Àâ±â – PART 6 ¢º ¢º Filter (¿©ÆÄ±â)

RF È¸·Î°³³ä Àâ±â – PART 6 ¢º ¢º Filter (¿©ÆÄ±â)

위키백과, 우리 모두의 백과사전

고주파필터와 저주파필터의 음양순환

1차 Low-Pass Filter(저주파 통과필터), High-Pass Filter(고주파 통과 필터) 구현하기, 코드

Leave a Comment Cancel reply

하이패스 필터 – 위키백과, 우리 모두의 백과사전

고주파필터와 저주파필터의 음양순환 : 네이버 블로그

1차 Low-Pass Filter(저주파 통과필터), High-Pass Filter(고주파 통과 필터) 구현하기, 코드

1차 Low-Pass Filter(저주파 통과필터), High-Pass Filter(고주파 통과 필터) 구현하기, 코드

KR100867850B1 – ê³ ì£¼í íí° ë° ê·¸ ì ì¡°ë°©ë² – Google Patents

RF È¸·Î°³³ä Àâ±â – PART 6 ¢º ¢º Filter (¿©ÆÄ±â)

RF È¸·Î°³³ä Àâ±â – PART 6 ¢º ¢º Filter (¿©ÆÄ±â)

위키백과, 우리 모두의 백과사전

고주파필터와 저주파필터의 음양순환

1차 Low-Pass Filter(저주파 통과필터), High-Pass Filter(고주파 통과 필터) 구현하기, 코드

Leave a Comment Cancel reply

KR100867850B1 – ê³ ì£¼í íí° ë° ê·¸ ì ì¡°ë°©ë²
– Google Patents