You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 삼각 측량 계산 on Google, you do not find the information you need! Here are the best content compiled and compiled by the Toplist.maxfit.vn team, along with other related topics such as: 삼각 측량 계산 삼각측량 gps, 삼각측량 삼변측량, 대삼각측량, 삼각측량 문제, 3차원 삼각측량, 삼각측량 예제, 삼각측량 종류, 비콘 삼각측량법
그 점과 두 기준점이 주어졌으면, 그 점과 두 기준점이 이루는 삼각형에서 밑변과 다른 두 변이 이루는 각을 각각 측정하고, 그 변의 길이를 측정한 뒤, 사인 법칙 등을 이용하여 일련의 계산을 수행함으로써, 그 점에 대해 좌표와 거리를 알아내는 방법이다.
삼각측량법 – 위키백과, 우리 모두의 백과사전
- Article author: ko.wikipedia.org
- Reviews from users: 23891
Ratings
- Top rated: 3.8
- Lowest rated: 1
- Summary of article content: Articles about 삼각측량법 – 위키백과, 우리 모두의 백과사전 Updating …
- Most searched keywords: Whether you are looking for 삼각측량법 – 위키백과, 우리 모두의 백과사전 Updating
- Table of Contents:
기본 원리[편집]
삼각망[편집]
순서[편집]
표지[편집]
편심 보정[편집]
조건[편집]
조정[편집]
같이 보기[편집]
외부 링크[편집]
각주[편집]
참고 문헌[편집]

삼각측량법 – 위키백과, 우리 모두의 백과사전
- Article author: hjiklee.sangji.ac.kr
- Reviews from users: 11450
Ratings
- Top rated: 3.3
- Lowest rated: 1
- Summary of article content: Articles about 삼각측량법 – 위키백과, 우리 모두의 백과사전 다음 삼각형은 계산된 변길이 a를 기선으로 활용. 삼각측량의 원리 : 수평위치(평면위치). – 최초 기선의 거리(c) 및 내각(수평각) 관측 (거리를 잴 수 없는 경우 삼각 … …
- Most searched keywords: Whether you are looking for 삼각측량법 – 위키백과, 우리 모두의 백과사전 다음 삼각형은 계산된 변길이 a를 기선으로 활용. 삼각측량의 원리 : 수평위치(평면위치). – 최초 기선의 거리(c) 및 내각(수평각) 관측 (거리를 잴 수 없는 경우 삼각 …
- Table of Contents:
기본 원리[편집]
삼각망[편집]
순서[편집]
표지[편집]
편심 보정[편집]
조건[편집]
조정[편집]
같이 보기[편집]
외부 링크[편집]
각주[편집]
참고 문헌[편집]

[측량학] 제 6장. 기준점 측량(삼각측량의 개요/방법/응용)#3
- Article author: knowledge-is-power.tistory.com
- Reviews from users: 19231
Ratings
- Top rated: 4.0
- Lowest rated: 1
- Summary of article content: Articles about [측량학] 제 6장. 기준점 측량(삼각측량의 개요/방법/응용)#3 2)삼변측량의 원리: 삼변측량은 코사인 제2법칙, 반각공식을 이용하여 변으로부터 각을 구하고 구한 각과 변에 의하여 수평위치가 결정되는데 관측값에 … …
- Most searched keywords: Whether you are looking for [측량학] 제 6장. 기준점 측량(삼각측량의 개요/방법/응용)#3 2)삼변측량의 원리: 삼변측량은 코사인 제2법칙, 반각공식을 이용하여 변으로부터 각을 구하고 구한 각과 변에 의하여 수평위치가 결정되는데 관측값에 … 5. 삼각측량의 개요 (1)삼각측량의 정의: 각종 측량의 골격이 되는 기준점인 삼각점의 위치를 삼각법으로 결정하기 위한 측량을 말하며 높은 정밀도를 요한다. (2)삼각점 선점시 주의사항 ·삼각형은 정삼각형에..
- Table of Contents:
관련글
댓글0
공지사항
최근댓글
태그
티스토리툴바
![[측량학] 제 6장. 기준점 측량(삼각측량의 개요/방법/응용)#3](https://img1.daumcdn.net/thumb/R800x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fr2QSg%2FbtqwA2Hoxmd%2F2YOOu0fC1hWzZc5HINCvok%2Fimg.png)
삼각측량(triangulation) | 과학문화포털 사이언스올
- Article author: www.scienceall.com
- Reviews from users: 5792
Ratings
- Top rated: 3.3
- Lowest rated: 1
- Summary of article content: Articles about 삼각측량(triangulation) | 과학문화포털 사이언스올 삼각측량은 크게 지구의 곡률을 고려한 엄밀한 관측과 복잡한 계산을 하는 대삼각측량과, 지표면을 평면으로 생각하고 하는 평면삼각측량으로 나뉜다. …
- Most searched keywords: Whether you are looking for 삼각측량(triangulation) | 과학문화포털 사이언스올 삼각측량은 크게 지구의 곡률을 고려한 엄밀한 관측과 복잡한 계산을 하는 대삼각측량과, 지표면을 평면으로 생각하고 하는 평면삼각측량으로 나뉜다. 과학의 모든 것! 과학 학습, 과학 체험, 과학 문화의 모든 것 사이언스올!지상측량법의 하나. 삼각측량은 측량할 지역에 적당한 크기의 삼각망(三角網)을 구성하여 각 삼각점(三角點)에서 삼각형의 내각과 삼각망중에서 한 변 또는 몇 개의 변의 길이를 실제로 측정하여 여기에서 각 삼각형의 변장(邊長)을 계산하고 각 삼각점의 위치를 정하는 측량이다.삼각측량
- Table of Contents:
See more articles in the same category here: Top 287 tips update new.
위키백과, 우리 모두의 백과사전
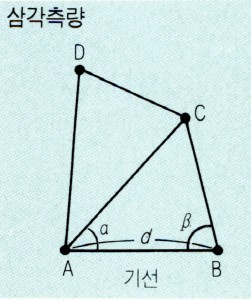
삼각측량법은 해변에서 배까지의 거리를 측정하는 데 활용될 수 있다. 관측자 A가 해변과 배 사이의 각도 α를 측정하고 관측자 B가 같은 식으로 각도 β를 구한다. A와 B사이의 거리 l이 주어지거나, A, B 각각의 좌표가 주어진다면, 사인 법칙 등을 이용하여 C에 위치한 배의 좌표를 알 수 있으며, 바닷가에서 배까지의 거리 d도 알아낼 수 있다.
삼각측량법은 측량 구역을 삼각형으로 분할하여 각 지점의 수평위치를 결정하는 측량법의 하나이다. 공공측량표준작업규정에서는 “1등, 2등, 3등, 4등 기본 삼각점 또는 기설 기준 삼각점을 기준으로 공공측량표준작업규정에서 정한 방법이나 정도로써 그 점의 위치를 결정하는 작업”이라고 정의한다. 그 점과 두 기준점이 주어졌으면, 그 점과 두 기준점이 이루는 삼각형에서 밑변과 다른 두 변이 이루는 각을 각각 측정하고, 그 변의 길이를 측정한 뒤, 사인 법칙 등을 이용하여 일련의 계산을 수행함으로써, 그 점에 대해 좌표와 거리를 알아내는 방법이다.
삼각측량법은 측량, 항해, 측정, 천체측량학, 로켓 공학 등에 쓰이며, 무기(대포 등)의 방향 설정에도 쓰인다.
(오른쪽 그림을 보면, 삼각형의 각 θ는 180-α-β이다. 삼각형의 내각의 합은 180도이기 때문이다. 이 각의 대변의 길이는 주어진 바 l이다. 사인법칙에 의해 sin(θ)/l이라는 비는 다른 각도 α와 β에 대해서도 동등하며, 나머지 두 변의 길이도 대수적으로 계산될 수 있다. 변의 길이를 구했으면 사인이나 코사인 값을 이용하여 점의 좌표를 알 수 있다.)
삼각측량은, 기준이 되는 한 변만 거리를 측정하고 나머지는 각만 측정하여 측점들의 위치를 계산하기 때문에, 멀리 떨어져 있는 점이라도 망원경으로 시준만 가능하다면 지형이나 거리에 제약에 관계 없이 측량을 할 수 있다는 장점이 있다.[3]
다음의 법칙들이 사용되었다. (유클리드 기하에서만 성립한다.)
기본 원리 [ 편집 ]
α, β 와 AB의 길이는 주어진다.
C는 거리 RC 혹은 MC를 이용해 구할 수 있다:
RC: 사인법칙과 코사인법칙을 이용하여 C의 위치를 구할 수 있다.
γ = 180 ∘ − α − β {\displaystyle \gamma =180^{\circ }-\alpha -\beta } sin α B C = sin β A C = sin γ A B {\displaystyle {\frac {\sin \alpha }{BC}}={\frac {\sin \beta }{AC}}={\frac {\sin \gamma }{AB}}}
AC와 BC를 다음과 같이 구할 수 있다.
A C = A B ⋅ sin β sin γ {\displaystyle AC={\frac {AB\cdot \sin \beta }{\sin \gamma }}} B C = A B ⋅ sin α sin γ {\displaystyle BC={\frac {AB\cdot \sin \alpha }{\sin \gamma }}}
RC는 다음과 같이 구할 수 있다.
R C = A C ⋅ sin α {\displaystyle RC=AC\cdot \sin \alpha } 혹은 R C = B C ⋅ sin β {\displaystyle RC=BC\cdot \sin \beta }
MC는 피타고라스 정리를 이용하여 구할 수 있다.
M R = A M − R B = ( A B 2 ) − ( B C ⋅ cos β ) {\displaystyle MR=AM-RB=\left({\frac {AB}{2}}\right)-\left(BC\cdot \cos \beta \right)} M C = M R 2 + R C 2 {\displaystyle MC={\sqrt {MR^{2}+RC^{2}}}}
삼각망 [ 편집 ]
삼각측량에 필요한 삼각점들을 연결하여 여러 개의 삼각형들이 만들어지는데 이를 삼각망이라 한다. 삼각망은 정삼각형에 가까운 것이 바람직하며 내각이 25 ~ 130도 사이에 있는 것이 좋다. 삼각망의 종류엔 단열 삼각망, 사변형 삼각망, 유심 삼각망이 있다.
용어
단열 삼각망
기선: 거리를 알고 있는 선으로 삼각측량의 출발선이 된다.
검기선: 거리를 알고 있는 선으로 측량 결과의 검정에 쓰인다.
각 이름
α: 다음 진행방향의 길이를 알고자 하는 선분을 마주보는 각을 α로 정한다.
β: 기지선을 마주보는 각을 β라고 한다.
γ: 나머지 각
단열 삼각망 [ 편집 ]
삼각형을 일렬로 연결하여 폭이 좁고 길이가 긴 형태로 만들면 단열 삼각망이 된다. 하천, 도로, 철도, 노선, 터널같은 폭이 좁고 길이가 긴 지형에 적합하게 쓰인다. 정밀도는 떨어지나 신속한 측량이 가능하다.
사변형 삼각망 [ 편집 ]
사변형 삼각망
삼각형을 연결하여 사변형으로 만든 다음, 사변형을 연속적으로 이어가는 형태를 사변형 삼각망, 또는 사변형망이라고 한다. 측량 면적이 작고 조건식 수가 많아 조정이 복잡하고 시간이 많이 걸리나, 정밀도가 높다. 폭이 좁고 길이가 긴 지형이면서 높은 정밀도를 요하는 경우 사용한다.
유심 삼각망 [ 편집 ]
유심 삼각망
삼각형의 측점 하나를 중심으로 삼각형이 둘러싸면서 측량하는 형태를 유심 삼각망이라고 한다. 방대한 지역의 측량에 적절하며, 단열 삼각망과 사변형망의 중간 정도 정밀도를 가진다.
순서 [ 편집 ]
계획: 삼각망 선정·배열, 작업일수 결정, 작업원 구성, 기계 선정, 경비 검토 등을 시행 준비: 관련 기관·토지 소유자 또는 관리자에게 미리 신고하고 허가를 받는다. 작업 공정표 작성, 기자재 점검, 경비 준비 등을 시행 답사(reconnaissance): 작업 예정 지역에 가서 현장 여건을 확인 선점(selecting station): 삼각점 설치 위치를 결정 조표(signal erection): 선점한 위치에 표지를 설치
표지 [ 편집 ]
대한민국의 영구표지
영국 Tirfergus Hill에 있는 영구표지
일시표지
카자흐스탄의 일시표지
표지는 삼각측량 이전에 미리 측점의 위치를 표시해두는 물건이다. 영구표지, 일시표지, 임시표지가 있다.
영구표지: 땅에 영구히 매설하는 표지. 석재 또는 합성수지를 쓴다. 삼각점 등급, 설치년도, 설치자 등의 정보가 새겨져 있다. 삼각점의 등급에 따라 영구표지의 치수가 다르다.
일시표지: 영구표지를 직접 시준할 수 없는 경우 종종 사용하는 목재 또는 철제 물체로, 영구표지 위에 높게 설치한다. 측표라고도 한다.
임시표지: 관측 기간동안만 설치하는 목재 또는 합성수지 말뚝이다. 깃발을 쓰는 경우 ‘표기’라고 부른다.
편심 보정 [ 편집 ]
기계의 위치, 영구표지의 위치, 측표의 위치는 정확히 연직선 상에 놓여야 편심에 의한 오차가 생기지 않는다. 그러나 실제 삼각측량을 하다보면 종종 현장 여건때문에 측표를 영구표지로부터 편심거리 e만큼 떨어뜨려 설치해야 하는 경우가 있다. 예를 들어 A점이 정확한 영구표지가 있는 점이라고 하고, B, C점에서 A점을 관측할 수 없어 P점에 측표를 세웠다고 할 경우, 편심 보정은 다음 과정으로 실시한다.
α ′ + β ′ + γ ′ = α + β + γ = 180 ∘ {\displaystyle \alpha ‘+\beta ‘+\gamma ‘=\alpha +\beta +\gamma =180^{\circ }} α ′ + β ′ − β = α + γ − γ ′ {\displaystyle \alpha ‘+\beta ‘-\beta =\alpha +\gamma -\gamma ‘} α ′ + δ β = α + δ γ {\displaystyle \alpha ‘+\delta _{\beta }=\alpha +\delta _{\gamma }} α ′ = α + δ γ − δ β {\displaystyle \alpha ‘=\alpha +\delta _{\gamma }-\delta _{\beta }}
여기서 α는 기지값, δ β , δ γ 는 미소한 값이므로, P B ¯ = l B , C P ¯ = l C {\displaystyle {\overline {PB}}=l_{B},{\overline {CP}}=l_{C}} 라 할 수 있고 사인법칙에 의해
δ β = sin ( 360 − φ ) e l B ρ ″ {\displaystyle \delta _{\beta }=\sin(360-\varphi ){\frac {e}{l_{B}}}\rho ”} δ γ = sin ( 360 − φ + α ) e l C ρ ″ {\displaystyle \delta _{\gamma }=\sin(360-\varphi +\alpha ){\frac {e}{l_{C}}}\rho ”}
∴ α ′ = α + sin ( 360 − φ + α ) e l C ρ ″ − sin ( 360 − φ ) e l B ρ ″ {\displaystyle \therefore \alpha ‘=\alpha +\sin(360-\varphi +\alpha ){\frac {e}{l_{C}}}\rho ”-\sin(360-\varphi ){\frac {e}{l_{B}}}\rho ”}
조건 [ 편집 ]
측량 결과가 허용오차 이내에 있는 경우 조건식을 이용하여 관측각을 조정하게 된다. 조건식은 각조건, 변조건, 점조건이 있다.
각조건: 삼각형의 내각의 합이 180°임을 이용
변조건: 삼각망의 임의 선분에 대해서, 어떤 경로를 거치든 계산 결과가 동일해야함을 이용. 예를 들어 단열삼각망에서 기선으로부터 계산하든, 검기선으로부터 계산하든 같은 선분에 대해서는 계산 결과가 같아야 한다.
점조건: 임의 한 점을 둘러싼 각의 총합은 360°임을 이용
조정 [ 편집 ]
삼각망의 종류에 따라 조정 방법이 약간씩 달라진다. 조정 과정 중 오차를 배분할 때 단위 또는 절단오차에 의해 정확하게 오차를 배분할 수 없는 경우가 있는데, 이때는 90°에 가까운 각에 잔여오차를 배분하는 것으로 한다. 예를 들어 10″를 세 각에 배분해야 할 때, 우선 3″씩 배분하고 남은 1″를 90°에 가장 가까운 한 각에 배분해준다.
사변형 망 조정 [ 편집 ]
사변형 망 조정에는 엄밀법과 근사법이 있다. 토목공학에서는 근사법이 더 간편하고 자주 사용된다.
각 조건은 다음 세 가지이다.
(1) + (2) = (5) + (6) (3) + (4) = (7) + (8) (1) + (2) + (3) + (4) + (5) + (6) + (7) + (8) = 360°
식의 좌우변이 같아야 오차가 없는 것이나, 오차가 생긴다고 하고, 각 식의 오차들을 ε 1 , ε 2 , ε 3 라고 하자. 같은 기계로, 같은 정도로 관측하는 경우 경중률이 없으므로 발생 오차를 관측 횟수로 나누어 균등분배한다. 즉, ϵ 1 4 , ϵ 2 4 , ϵ 3 8 {\displaystyle {\frac {\epsilon _{1}}{4}},{\frac {\epsilon _{2}}{4}},{\frac {\epsilon _{3}}{8}}} 씩 배분하여 조정각을 구한다.
(1)의 조정각 = ( 1 ) ∓ ϵ 1 4 ∓ ϵ 3 8 {\displaystyle =(1)\mp {\frac {\epsilon _{1}}{4}}\mp {\frac {\epsilon _{3}}{8}}}
(2)의 조정각 = ( 2 ) ∓ ϵ 1 4 ∓ ϵ 3 8 {\displaystyle =(2)\mp {\frac {\epsilon _{1}}{4}}\mp {\frac {\epsilon _{3}}{8}}}
(3)의 조정각 = ( 3 ) ∓ ϵ 2 4 ∓ ϵ 3 8 {\displaystyle =(3)\mp {\frac {\epsilon _{2}}{4}}\mp {\frac {\epsilon _{3}}{8}}}
(4)의 조정각 = ( 4 ) ∓ ϵ 2 4 ∓ ϵ 3 8 {\displaystyle =(4)\mp {\frac {\epsilon _{2}}{4}}\mp {\frac {\epsilon _{3}}{8}}}
(5)의 조정각 = ( 5 ) ∓ ϵ 1 4 ∓ ϵ 3 8 {\displaystyle =(5)\mp {\frac {\epsilon _{1}}{4}}\mp {\frac {\epsilon _{3}}{8}}}
(6)의 조정각 = ( 6 ) ∓ ϵ 1 4 ∓ ϵ 3 8 {\displaystyle =(6)\mp {\frac {\epsilon _{1}}{4}}\mp {\frac {\epsilon _{3}}{8}}}
(7)의 조정각 = ( 7 ) ∓ ϵ 2 4 ∓ ϵ 3 8 {\displaystyle =(7)\mp {\frac {\epsilon _{2}}{4}}\mp {\frac {\epsilon _{3}}{8}}}
(8)의 조정각 = ( 8 ) ∓ ϵ 2 4 ∓ ϵ 3 8 {\displaystyle =(8)\mp {\frac {\epsilon _{2}}{4}}\mp {\frac {\epsilon _{3}}{8}}}
변조건에 의한 조정은 우선 각조건에 의해 조정된 조정각에 log sin을 취한 후 10을 더하고, 다음으로 정의되는 표차(tabular difference, d)를 구한다. 표차는 소수점 아래 8자리에서 반올림하여 7자리까지 나타낸다.
d i = 2.106 × 10 − 6 cot (조 정 각 ) {\displaystyle d_{i}=2.106\times 10^{-6}\cot {\text{(조 정 각 )}}}
다음으로 ε 4 를 구한다.
ϵ 4 = Σ ( log sin 홀 수 각 + 10 ) − Σ ( log sin 짝 수 각 + 10 ) {\displaystyle \epsilon _{4}=\Sigma (\log \sin {\text{홀 수 각}}+10)-\Sigma (\log \sin {\text{짝 수 각}}+10)}
변조건 조정량은 ϵ 4 Σ d {\displaystyle {\frac {\epsilon _{4}}{\Sigma d}}} 이며, 이 값을 ε 4 가 음수이면 홀수각에 조정량만큼 더해주고, 짝수각에는 조정량만큼 빼주면 된다. 변조건 조정까지 끝났으면 각들을 다 더해서 내각의 합인 360°가 나오는지 확인한다. 점조건은 사변형 망에서 사용되지 않는다.
단열삼각망 조정 [ 편집 ]
각조건은 삼각형 내각의 합은 180°임을 이용한다. 삼각망을 구성하는 각각의 삼각형 내각의 합을 구한 뒤, 180°와의 차이만큼 삼각형을 이루는 세 각에 분배해준다.
방향각조건에 의한 조정은 검기선의 방향각 기지값이, 기선으로부터 계산해서 나온 검기선 방향각과 동일해야 한다는 것을 근거로 실시한다. 방향각은 다음 원리로 계산된다. (n은 삼각형 수)
현재 측선 방향각 = 전 측선 방향각 + 180 ± 교각 (진행방향에 대해 왼쪽방향 교각은 더해주고, 오른쪽방향 교각은 빼준다) 계산을 통한 검기선 방향각 = 기 선 방 향 각 + 180 n + Σ γ 진 행 방 향 왼 쪽 − Σ γ 진 행 방 향 오 른 쪽 {\displaystyle ={\text{기 선 방 향 각}}+180n+\Sigma \gamma _{\text{진 행 방 향 왼 쪽}}-\Sigma \gamma _{\text{진 행 방 향 오 른 쪽}}} 오차 ϵ 2 = 계 산 을 통 한 검 기 선 방 향 각 − 기 지 값 검 기 선 방 향 각 {\displaystyle \epsilon _{2}={\text{계 산 을 통 한 검 기 선 방 향 각 }}-{\text{기 지 값 검 기 선 방 향 각 }}}
α, β, γ각에 대해 조정량은 다음과 같다.
ν α = ϵ 2 2 n {\displaystyle
u _{\alpha }={\frac {\epsilon _{2}}{2n}}} ν β = ϵ 2 2 n {\displaystyle
u _{\beta }={\frac {\epsilon _{2}}{2n}}} ν γ = ϵ 2 n {\displaystyle
u _{\gamma }={\frac {\epsilon _{2}}{n}}}
다음으로 변조건에 의한 조정을 실시한다. 변조건에 의한 조정은 γ를 제외하고 α, β에 대해서만 실시한다. 첫번째 측선 길이를 L 1 , n번째 측선 길이를 L n 이라 할 때
ϵ 3 = log L 1 − log L n + Σ log sin α − Σ log sin β {\displaystyle \epsilon _{3}=\log L_{1}-\log L_{n}+\Sigma \log \sin \alpha -\Sigma \log \sin \beta } ν 4 = ν α = ν β = ϵ 3 Σ d {\displaystyle
u _{4}=
u _{\alpha }=
u _{\beta }={\frac {\epsilon _{3}}{\Sigma d}}}
조정량 ν 4 를 적용한 조정각을 구했으면 삼각형마다 사인법칙을 적용하여 변 길이를 구한다.
유심다각망 조정 [ 편집 ]
유심다각망은 각조건, 방향각조건, 측점조건, 변조건에 의한 조정을 해준다. 각조건은 각 삼각형의 내각의 합이 180도가 되어야 한다는 것이다. 단열삼각망에서와 같은 방법으로 조정한다.
방향각조건에 의한 조정은 기선의 방향각을 기초로 계산한 각 변의 방향각이 이미 알고 있는 방향각과 같아야 한다는 것을 이용하여 실시한다. 오차가 발생하고, 정도가 같은 측정을 했다면 보정량 ν 2 는 마지막 측선까지 중심각 수 n으로 과부족량 ε 2 를 나누어주어 분배한다.
ν 2 = ϵ 2 n {\displaystyle
u _{2}={\frac {\epsilon _{2}}{n}}}
측점조건에 의한 조정은 다각형 중앙의 점 주위의 각을 모두 합하면 360도가 되어야한다는 것을 이용한다. 360도가 안 된다면 과부족량을 중심각 수 n으로 나누어서 조정해준다.
변조건에 의한 조정은 처음 기선의 길이와 계산을 통해 최종적으로 얻는 같은 위치의 변 길이가 같아야 한다는 것을 이용한다. 조정할 때는 중심각은 계산에 사용되지 않는다. 즉 삼각형 부분에서 다각형의 중심을 구성하는 각을 제외한 나머지 두 각만 이용한다. 기선의 길이를 b 1 , 계산을 통해 나온 변 길이가 b n , 다각형의 가장자리를 구성하는 두 각을 α i , β i 라고 하면 다음 과정으로 조정을 진행한다.
b n = sin α 1 sin α 2 ⋯ sin α n sin β 1 sin β 2 ⋯ sin β n b 1 {\displaystyle b_{n}={\frac {\sin \alpha _{1}\sin \alpha _{2}\cdots \sin \alpha _{n}}{\sin \beta _{1}\sin \beta _{2}\cdots \sin \beta _{n}}}b_{1}}
b 1 , b n 은 서로 같아야 한다. 즉
b n b 1 = 1 = sin α 1 sin α 2 ⋯ sin α n sin β 1 sin β 2 ⋯ sin β n {\displaystyle {\frac {b_{n}}{b_{1}}}=1={\frac {\sin \alpha _{1}\sin \alpha _{2}\cdots \sin \alpha _{n}}{\sin \beta _{1}\sin \beta _{2}\cdots \sin \beta _{n}}}}
양변에 로그를 취하여 변조건에 의해 발생하는 오차 ε 4 를 계산한다.
∑ log sin α − ∑ log sin β = ϵ 4 {\displaystyle \sum \log \sin \alpha -\sum \log \sin \beta =\epsilon _{4}}
표차 d를 계산하고, 조정량을 계산한다.
ν α , β = ϵ 4 ∑ d {\displaystyle
u _{\alpha ,\beta }={\frac {\epsilon _{4}}{\sum d}}}
같이 보기 [ 편집 ]
외부 링크 [ 편집 ]
위키미디어 공용에 관련 미디어 분류가 있습니다.
위키미디어 공용에 관련 미디어 분류가 있습니다. 위키배움터에 삼각측량 관련 자료가 있습니다.
위키배움터에 삼각측량 관련 자료가 있습니다. 국토지리정보원: 정보 다운로드에서 여러 삼각점의 정보를 볼 수 있다.
각주 [ 편집 ]
[측량학] 제 6장. 기준점 측량(삼각측량의 개요/방법/응용)#3
5. 삼각측량의 개요
(1)삼각측량의 정의: 각종 측량의 골격이 되는 기준점인 삼각점의 위치를 삼각법으로 결정하기 위한 측량을 말하며 높은 정밀도를 요한다 .
(2)삼각점 선점시 주의사항
·삼각형은 정삼각형에 가까울수록 좋다.
·가능한 측점수를 적게하고 측점간 거리는 같을수록 좋다.
·미지점은 최소 3개, 최대 5개의 기지점에서 정, 반 양방향으로 시통이 되도록 한다 .
·다른 삼각점과 시준이 잘되어야 한다 .
(3)삼각측량의 원리: sin법칙에 의한다.
(4)삼각망의 종류
:삼각망 중에서 임의의 한 변의 길이는 계산의 순서에 관계없이 동일해야하며, 각 삼각형 내각의 합은 180가 되도록 한다.
1)단열 삼각망: 하천, 도로, 터널측량 등 좁고 긴 지역에 적합하며 경제적이나 정도가 낮다.
2)유심 삼각망: 측점수에 비해 피복면적이 가장 넓고 정밀도도 좋다.
3)사변형 삼각망: 가장 정도가 높으나 피복면적이 작아 비경제적이므로 중요한 기선 삼각망에 사용한다.
(5)편심관측
:삼각측량에서 수평각 관측은 삼각점에 기계를 세워 다른 삼각점을 시준해서 실시하나 부득이 하게 삼각점에 기계를 세우지 못하거나 , 삼각점을 시준하지 못하고 편심시켜 관측해서 정확한 값을 계산해내는 방법, A점에 기계를 세우지 못하고 B점에 기계를 세운 경우
6. 삼각측량의 방법
(1)조건식의 수
1)측점조건식의 수
유심삼각망만 1이 나온다.
2)변 조건식의 수
단열삼각망은 기선과 점기선이 같이 있을때만 1개이다.
3)각 조건식의 수
삼각형의 수
4)조건식의 총수
(2)단열 삼각망의 조정
1)각조건의 조정
①제1조정: 삼각형의 내각의 합이 180가 되도록 조정한다.
②제2조정: 방위각에 대한 조건을 만족하도록 조정한다.
(3)유심 삼각망의 조정
1)각 조건의 조정
①제 1조정: 단열삼각망과 동일
(4)사변형 삼각망의 조정
1)각 조건의 조정
①제 1조정: 사변형 내각의 합이 360가 되도록 조정
②제 2조정: 맞꼭지각은 같도록 조정
※각의 크기에 관계 없이 등배분하여 조정한다.
728×90
7. 삼각측량의 응용
(1)삼각 수준측량
1)곡률오차(구차): 구차는 실제 높이보다 측정높이가 적게 나타나므로 +해준다.
2)기차(굴절오차): 기차는 실제 높이보다 더 크게 나타나므로 -해준다.
3)양차: 기차와 구차를 합한 값
(2)삼변측량
1)정의: 전자파거리 측정기를 이용 한 정밀한 장거리 측정으로 변장을 측정해서 삼각점의 위치를 결정하는 측량방법
2)삼변측량의 원리: 삼변측량은 코사인 제2법칙, 반각공식을 이용하여 변으로부터 각을 구하고 구한 각과 변에 의하여 수평위치가 결정되는데 관측값에 비하여 조건식이 적은 것이 단점 이다.
3)삼변측량의 특징
· 삼변을 측정해서 삼각점의 위치를 결정 한다.
·기선장을 실측하므로 기선의 확대가 불필요하다.
· 조건식의 수가 적은 것이 단점 이다.
· 좌표계산이 편리 하다.
·조정방법에는 조건방정식에 의한 조정과 관측방정식에 의한 조정이 있다.
4)수평각의 계산
728×90
반응형
So you have finished reading the 삼각 측량 계산 topic article, if you find this article useful, please share it. Thank you very much. See more: 삼각측량 gps, 삼각측량 삼변측량, 대삼각측량, 삼각측량 문제, 3차원 삼각측량, 삼각측량 예제, 삼각측량 종류, 비콘 삼각측량법
