Top 47 1 차 저역 통과 필터 Top Answer Update

You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 1 차 저역 통과 필터 on Google, you do not find the information you need! Here are the best content compiled and compiled by the Toplist.maxfit.vn team, along with other related topics such as: 1 차 저역 통과 필터 2차 저역통과필터, 능동 저역 통과 필터, LPF 필터, 1차 low pass filter, 로우패스필터 코드, 저역통과필터 차단주파수, Low Pass filter 수식, 저역통과필터 원리

16. Electric and Electronic Basic. Types of Electric Filters and 1st RC Low pass Filters Design

1차 Low-Pass Filter(저주파 통과필터), High-Pass Filter(고주파 통과 필터) 구현하기, 코드

Article author: ddangeun.tistory.com
Reviews from users: 33459 Ratings
Top rated: 4.3
Lowest rated: 1
Summary of article content: Articles about 1차 Low-Pass Filter(저주파 통과필터), High-Pass Filter(고주파 통과 필터) 구현하기, 코드 1차 Low-Pass Filter … lpf는 말그대로 신호의 낮은 주파수 부분을 통과시키는 건데요, 즉 신호의 높은 주파수(예를 들어 진동이나 노이즈)를 없애 신호를 … …
Most searched keywords: Whether you are looking for 1차 Low-Pass Filter(저주파 통과필터), High-Pass Filter(고주파 통과 필터) 구현하기, 코드 1차 Low-Pass Filter … lpf는 말그대로 신호의 낮은 주파수 부분을 통과시키는 건데요, 즉 신호의 높은 주파수(예를 들어 진동이나 노이즈)를 없애 신호를 … 저주파 통과필터(Low-Pass Filter), 고주파 통과필터 (High-Pass Filter)를 이하 lpf, hpf라 부르겠습니다. 신호 처리를 함에 있어 원하는 신호를 뽑아내기 위해 lpf와 hpf를 사용하여 지지고 볶았습니다. 어느정..
Table of Contents:

‘공통 이론’ Related Articles

공지사항

최근 포스트

검색

전체 방문자

티스토리툴바

1차 Low-Pass Filter(저주파 통과필터), High-Pass Filter(고주파 통과 필터) 구현하기, 코드

Article author: m.blog.naver.com
Reviews from users: 43681 Ratings
Top rated: 4.2
Lowest rated: 1
Summary of article content: Articles about 1차 수동 필터 – 저역 통과 필터(LPF), 고역통과필터(HPF) : 네이버 블로그 이미 필터를 설계하고자 이 글을 검색해서 들어오시는 분들은 이미 회로이론 1,2를 배운 입장일테니 전달함수 구하는 것쯤은 할수 있다고 가정하고 결과만 … …
Most searched keywords: Whether you are looking for 1차 수동 필터 – 저역 통과 필터(LPF), 고역통과필터(HPF) : 네이버 블로그 이미 필터를 설계하고자 이 글을 검색해서 들어오시는 분들은 이미 회로이론 1,2를 배운 입장일테니 전달함수 구하는 것쯤은 할수 있다고 가정하고 결과만 …
Table of Contents:

카테고리 이동

전자회로저장소

이 블로그
Analog filter
카테고리 글

카테고리

이 블로그
Analog filter
카테고리 글

1차 수동 필터 - 저역 통과 필터(LPF), 고역통과필터(HPF) : 네이버 블로그 — 1차 수동 필터 – 저역 통과 필터(LPF), 고역통과필터(HPF) : 네이버 블로그

Article author: circuit-designer.tistory.com
Reviews from users: 47928 Ratings
Top rated: 4.4
Lowest rated: 1
Summary of article content: Articles about [회로 기초] 능동 저역통과 필터(Low-pass filter)에 대해 알아보자 간단히 얘기하면 주파수가 낮은 영역의 출력은 통과하고 주파수가 높아지면 출력을 차단하는 역할을 한다. 연산 증폭기를 사용한 1차 저역통과 필터는 … …
Most searched keywords: Whether you are looking for [회로 기초] 능동 저역통과 필터(Low-pass filter)에 대해 알아보자 간단히 얘기하면 주파수가 낮은 영역의 출력은 통과하고 주파수가 높아지면 출력을 차단하는 역할을 한다. 연산 증폭기를 사용한 1차 저역통과 필터는 … 능동 필터 회로 앞 장에서 본 필터 회로들(LPF, HPF, 대역 통과 필터, 대역 차단 필터)은 수동 소자인 저항, 인덕터, 커패시터로 이루어진 회로이다. 이를 수동 필터 회로라고 하며 연산 증폭기(OP amp)를 사용하..전자 회로에 대한 내용들을 공유하는 블로그입니다.
Table of Contents:

[회로 기초] 능동 저역통과 필터(Low-pass filter)에 대해 알아보자

티스토리툴바

Article author: ko.wikipedia.org
Reviews from users: 45930 Ratings
Top rated: 3.4
Lowest rated: 1
Summary of article content: Articles about 로우패스 필터 – 위키백과, 우리 모두의 백과사전 필터의 세부적인 주파수 응답은 필터 설계에 따라 달라진다. 이러한 저주파 통과 필터는 종종 오디오 부문에서 고주파 차단 필터(high-cut filter)나 고역 차단 필터( … …
Most searched keywords: Whether you are looking for 로우패스 필터 – 위키백과, 우리 모두의 백과사전 필터의 세부적인 주파수 응답은 필터 설계에 따라 달라진다. 이러한 저주파 통과 필터는 종종 오디오 부문에서 고주파 차단 필터(high-cut filter)나 고역 차단 필터( …
Table of Contents:

이상적인 필터와 현실적인 필터[편집]

시간 응답[편집]

주파수 응답[편집]

이산 시간 샘플링의 미분방정식[편집]

전기 회로[편집]

같이 보기[편집]

각주[편집]

외부 링크[편집]

Article author: www.ktword.co.kr
Reviews from users: 34440 Ratings
Top rated: 3.9
Lowest rated: 1
Summary of article content: Articles about 1차 LPF [정보통신기술용어해설] 1차 LPF의 RC 회로 구현 ☞ LPF RC 회로, 지상회로(Lag Circuit) 참조 ㅇ RC 1차 회로에 의해 LPF(저역통과필터)를 구현하는 간단한 회로 … …
Most searched keywords: Whether you are looking for 1차 LPF [정보통신기술용어해설] 1차 LPF의 RC 회로 구현 ☞ LPF RC 회로, 지상회로(Lag Circuit) 참조 ㅇ RC 1차 회로에 의해 LPF(저역통과필터)를 구현하는 간단한 회로 … 정보통신용어,정보통신사전,차재복
Table of Contents:

1차 LPF [정보통신기술용어해설]

Article author: pinkwink.kr
Reviews from users: 31539 Ratings
Top rated: 3.6
Lowest rated: 1
Summary of article content: Articles about [필터연재] 1차 디지털 저역/고역 통과필터 오늘 다룰 이야기는 1차 저역 통과필터와 1차 고역 통과필터 흔히 LPF(Low Pass Filter), HPF(High Pass Filter)에 대한 이야기 입니다. 흔히 Hz 단위의 … …
Most searched keywords: Whether you are looking for [필터연재] 1차 디지털 저역/고역 통과필터 오늘 다룰 이야기는 1차 저역 통과필터와 1차 고역 통과필터 흔히 LPF(Low Pass Filter), HPF(High Pass Filter)에 대한 이야기 입니다. 흔히 Hz 단위의 … 전 아주 예전부터 제 블로그에 필터에 관한 글을 올리고 있었습니다. 물론 단편적인 글들이었지만요. 그 중에는 실제 자이로센서와 가속도센서를 융합하는 상보필터[바로가기]를 다루기 시작했고, 그 후 MATLAB이..
Table of Contents:

태그

‘TheoryControlTheory’ Related Articles

Article author: cms3.koreatech.ac.kr
Reviews from users: 21498 Ratings
Top rated: 4.4
Lowest rated: 1
Summary of article content: Articles about [필터연재] 1차 디지털 저역/고역 통과필터 1차필터(First-order filter). • 2차 LPF (Second order Low Pass Filter). • 고차필터(Higher order filters). • 다중궤환 대역통과필터(MFB bandpass filters). …
Most searched keywords: Whether you are looking for [필터연재] 1차 디지털 저역/고역 통과필터 1차필터(First-order filter). • 2차 LPF (Second order Low Pass Filter). • 고차필터(Higher order filters). • 다중궤환 대역통과필터(MFB bandpass filters). 전 아주 예전부터 제 블로그에 필터에 관한 글을 올리고 있었습니다. 물론 단편적인 글들이었지만요. 그 중에는 실제 자이로센서와 가속도센서를 융합하는 상보필터[바로가기]를 다루기 시작했고, 그 후 MATLAB이..
Table of Contents:

태그

‘TheoryControlTheory’ Related Articles

Article author: eunkyovely.tistory.com
Reviews from users: 37368 Ratings
Top rated: 3.1
Lowest rated: 1
Summary of article content: Articles about RC Low pass filter (LPF)란? Low pass filter LPF란 말 그대로 저주파를 통과시키는 필터를 얘기합니다. ; 위 그림은 전형적인 1차 low pass filter 회로입니다. 커패시터가 고주파 … …
Most searched keywords: Whether you are looking for RC Low pass filter (LPF)란? Low pass filter LPF란 말 그대로 저주파를 통과시키는 필터를 얘기합니다. ; 위 그림은 전형적인 1차 low pass filter 회로입니다. 커패시터가 고주파 … 안녕하세요 오늘은 Low pass filter에 대해서 공부하고 정리해보겠습니다. RC lowpass filter RC(resistor-capacitor) 회로는 저항과 커패시터로 구성된 회로로써 Low pass filter LPF 그리고 High pass filter HP..
Table of Contents:

RC lowpass filter

태그

공지사항

최근글

1차 Low-Pass Filter(저주파 통과필터), High-Pass Filter(고주파 통과 필터) 구현하기, 코드

728×90

반응형

저주파 통과필터(Low-Pass Filter), 고주파 통과필터 (High-Pass Filter)를 이하 lpf, hpf라 부르겠습니다.

신호 처리를 함에 있어 원하는 신호를 뽑아내기 위해 lpf와 hpf를 사용하여 지지고 볶았습니다.

어느정도 원리를 깨달았죠.. 코드만 원하시면 밑으로 가면 됩니다. ㅎㅎ

<칼만필터는 어렵지 않아> 책을 참고하였습니다.

1차 Low-Pass Filter

lpf는 말그대로 신호의 낮은 주파수 부분을 통과시키는 건데요, 즉 신호의 높은 주파수(예를 들어 진동이나 노이즈)를 없애 신호를 좀더 매끄럽게 만들어 줍니다. 그러므로 자주 사용되죠.

이런식으로 효과를 볼 수 있습니다.

Smoothing이라고도 하죠. 그냥 lpf입니다.

단순히 생각하면 lpf를 만들기 위해선 이전 측정값과 현재 측정값에 가중치를 두어 계산하면 됩니다.

다시말하면, 이전 값을 고려하여 현재값을 정하고, 이전값에 어느정도 비중을 둔 현재값을 계산하면 됩니다.

α는 1에서 0사이의 값이고, x_k는 k번째 측정값, x바는 계산된 값(추정값, lpf 필터된 값)입니다.

α가 클수록 이전 값에 비중이 커져 더 그래프가 부드러워지고, 잡음이 줄어듭니다. 하지만 반대로 실제 값과는 달라지게 되겠죠.

하지만 시간 영역에서 α를 설계하기는 쉽지 않습니다. 보통 차단주파수를 정해 lpf를 사용하는데, 이를 위해 시간영역의 식을 주파수 영역의 식으로 바꾸어 주면 됩니다.

이는 라플라스 변환 식을 사용하면 됩니다.

위의 식이 라플라스 변환 식입니다. 간단히 대입만 해주면 됩니다.

lpf의 시간영역식과 라플라스 변환한 주파수 영역의 식은 다음과 같이 나타낼 수 있습니다.

여기서 G(s)는 output/iniput의 형태로 나타내고, 전달함수라고 부릅니다.

간단한 lpf 필터 전달함수는 다음과 같이 나타낼 수 있습니다.

이 식은 1차 lpf 회로에서 나왔습니다.

키르히호프 전압법칙에 의해 미분방정식이 나옵니다.

주파수 영역으로 바꾸어줍니다.

전달함수를 구합니다.

또한 전달함수의 s(주파수)가 0이나 무한대로 갈때 어디로 수렴하는지 보면 lpf인지, hpf인지 알 수 있습니다.

낮은 주파수를 통과하는 저주파 통과 필터인 것을 알 수 있습니다.

위의 전달 함수를 다시 다음과 같이 써줍니다.

위의 식을 라플라스 역변환 합니다. s가 곱해지면 미분함수가 되므로, 다음과 같이 쓸 수 있습니다.

이산 신호인것을 고려하여 다음과 같이 바꾸어 줍니다.

위와 같이 1차 lpf 식을 만들 수 있습니다.

// lowpass filter float lpf(float x_k, float y_km1, float Ts, float tau) { float y_k; y_k = (tau * y_km1 + Ts * x_k) / (Ts + tau); return y_k; }

위 식을 보면, 알파는 다음과 같음을 알 수 있습니다.

τ(tau)는 다음과 같이 정해집니다.

w_cut은차단 각주파수(rad/s), f_cut은 차단주파수(Hz)입니다.

1차 High-Pass Filter

hpf는 신호의 변화만 캐치하는데 효과적입니다.

예를들어 적분시 발생하는 적분 상수를 제거한다던지, 0Hz의 전압이나 offset 등을 제거하는데 사용하곤 했습니다.

lpf처럼 hpf도 다음과 같이 전달함수를 쓸 수 있습니다.

높은 주파수의 신호만 통과하는 것을 확인할 수 있습니다.

이제 라플라스 역변환후, 이산신호의 식으로 바꾸어 줍니다.

// highpass filter float hpf(float x_k, float x_km1, float y_km1, float Ts, float tau) { float y_k; y_k = (tau/(tau + Ts) * y_km1) + (tau/(tau + Ts)) * (x_k – x_km1); return y_k; }

끝!^^

728×90

반응형

[회로 기초] 능동 저역통과 필터(Low-pass filter)에 대해 알아보자

능동 필터 회로

앞 장에서 본 필터 회로들(LPF, HPF, 대역 통과 필터, 대역 차단 필터)은 수동 소자인 저항, 인덕터, 커패시터로 이루어진 회로이다. 이를 수동 필터 회로라고 하며 연산 증폭기(OP amp)를 사용하여 필터 회로들을 만들 수 있는데 이 필터 회로들은 능동 필터 회로라고 한다. 능동 필터 회로는 수동 필터 회로에 비해 가지는 장점은 인덕터의 유무이다. 인덕터는 보통 크고, 무겁고, 비싸며, 원하는 주파수 응답 특성을 상쇄시킬 수도 있는 전자장 효과를 발생시킨다. 수동 필터 회로의 경우에는 회로 구성을 위해 이런 인덕터가 필요하지만, 능동 필터 회로의 경우 회로 구성에 인덕터를 사용하지 않고 필터 회로를 구성할 수 있다. 연산 증폭기(OP amp)로 구성된 능동 필터를 살펴보자.

1차 저역통과 필터(Low-pass filter)

저역 통과 필터(Low-pass filter)의 특징에 대해서는 앞에서 살펴보았다. 간단히 얘기하면 주파수가 낮은 영역의 출력은 통과하고 주파수가 높아지면 출력을 차단하는 역할을 한다.

연산 증폭기를 사용한 1차 저역통과 필터는 아래와 같다.

1차 저역 통과 필터

위의 회로가 어떻게 저역 통과 필터로 동작하는지 살펴보자.

먼저 연산 증폭기는 Ideal OP amp로 가정하고 전달 함수를 확인해보자.

Ideal OP amp의 특징으로 V n 의 전압과 V p 의 전압이 같고 V n 의 전압은 V p 의 전압을 따라 0V가 됨을 알 수 있다.

또한 Vn을 기준으로 KCL을 적용할 수 있는데 이를 표현한 식은 다음과 같다.

위의 식에 앞에서 구한 V n 의 값을 사용해 표현하면 아래 식으로 표현할 수 있다.

커패시터에 흐르는 전류를 쉽게 구하기 위해 주파수 영역의 식을 적었다.

위의 식을 사용해 전달 함수를 표현하려면 아래와 같이 식을 풀면 된다.

전달 함수 H(s)는 다음과 같다.

전달 함수 H(s)를 이전에 본 저역 통과 필터의 일반식의 형태와 비슷한 형태로 맞춰보면 다음과 같이 나타낼 수 있다.

위의 식에서 보면 알 수 있듯이 저역 통과 필터의 일반식의 형태와 비슷하다.

다른 점이 있다면 통과 대역의 이득인 K가 R 2 /R 1 의 비로 결정된다는 점이다.

이런 방식으로 고역 통과 필터도 해석할 수 있다. 능동 고역 통과 필터는 다음 장에서 해석해보자.

반응형

위키백과, 우리 모두의 백과사전

현실적인 저주파 통과 필터 중 하나인 RC 필터의 다이어그램.

로우패스 필터(Low-pass filter, LPF) 또는 저주파 통과 필터는 특정한 차단 주파수 이상 주파수의 신호를 감쇠시켜 차단 주파수 이하의 주파수 신호만 통과시키는 필터를 의미한다.[1] 필터의 세부적인 주파수 응답은 필터 설계에 따라 달라진다. 이러한 저주파 통과 필터는 종종 오디오 부문에서 고주파 차단 필터(high-cut filter)나 고역 차단 필터(treble-cut filter)이라 부르기도 한다. 저주파 통과 필터와 반대의 기능을 하는 필터로 고주파 통과 필터가 있다.[2]
광학에서는 “하이 패스”(High-pass)와 “로우 패스”(Low-pass)가 주파수와 빛의 파장 중 어느 쪽에 속하느냐에 따라서 서로 다른 의미를 가질 수 있다. 주파수의 하이 패스 필터(고주파 통과 필터)는 파장의 로우 패스 필터가 되며, 반대로 주파수의 로우 패스 필터(저주파 통과 필터)는 파장의 하이 패스 필터가 될 수 있다. 이 때문에 광학에서 파장 필터는 혼란을 막기 위해 로우 패스/하이 패스 대신 롱 패스(Long-pass), 숏 패스(Short-pass)라고 부른다.[3]
저주파 통과 필터는 단시간에 튀어나오는 잡음 성분인 고주파 성분을 제거하고 장기 추세 신호만 통과시키기 때문에 보다 신호를 부드럽게 만들 때 사용된다. 보통 음성에 사용되는 히스 필터나 아날로그-디지털 변환 중 신호 전처리를 위한 안티에일리어싱 필터, 데이터 세트 평활화를 위한 디지털 필터, 가우시안 블러 등 다양한 분야에서 응용된다.[4] 또한 금융 분야에 사용되는 이동평균필터 또한 특정한 종류의 저주파 통과 필터에 해당되며, 다른 저주파 통과 필터에 사용하는 것과 같은 신호 처리 기술로 분석할 수 있다.[5]
이상적인 필터와 현실적인 필터 [ 편집 ]
1차 저주파 통과 필터의 크기 이득 주파수 응답 그래프. 신호 이득은 데시벨 단위로 표기한다. 예를 들어 차단 주파수 이상에서는 신호가 3dB의 기울기로 감쇠된다. 각진동수 는 초당 라디안(rad/s) 단위로, 로그 척도로 그려저 있다.

이상적인 저주파 통과 필터는 차단 주파수 이상의 주파수 대역 신호는 완전히 차단하고 그 이하의 주파수 대역 신호는 완전히 통과시키는 필터로, 이 필터의 주파수 응답은 구형함수 모양의 “벽돌담 필터”에 해당한다. 실제 필터에 존재하는 전이 대역이 이상적인 필터에서는 존재하지 않는다. 이상적인 저대역 통과 필터는 수학적으로 주파수 영역에서 구형함수에 신호를 곱하거나 시간 영역에서 임펄스 응답과 싱크함수를 합성곱(컨볼루션) 하는 방법으로 만들 수 있다.[6]
하지만 싱크함수 자체의 정의역이 음의 무한대 시간부터 양의 무한대 시간까지 존재하기 때문에 이상적인 필터는 무한한 시간 범위의 신호를 가져야만 만들 수 있어 구현하는 것이 물리적으로 불가능하기 때문에 보통은 실제 진행중인 신호에 대해 근사적으로만 구현할 수 있다. 그러므로 필터가 완벽한 컨볼루션을 하기 위해서는 무한한 지연 시간을 가지거나 무한한 과거와 미래에 대한 신호가 무엇인지 알고 있어야 한다. 일반적으로는 머나먼 과거와 미래의 신호를 0이라고 가정하여 사전에 만들어진 디지털 신호를 만들거나 신호를 반복해 만들어 푸리에 해석을 사용하는 방식으로 해결한다.[6]
현실 세계에서 사용하는 현실적인 필터는 무한 임펄스 응답을 잘라내고 윈도우 함수를 사용해 유한 임펄스 응답을 만들어 이상적인 필터와 비슷하게 구현한다. 이 필터를 실제로 적용하러면 약간의 시간이 흐른 후의 “미래를 봐야만” 구현되므로 필터의 출력 신호는 약간 지연되어 나온다. 이 때 응답 신호의 지연은 위상 지연으로 나타난다. 근사치의 정확도를 높이기 위해서는 지연도 더 길어져야 한다.[7]
이상적인 저주파 통과 필터는 깁스 효과로 인해 링잉 아티팩트가 나타난다. 윈도우 함수를 어떻게 선택하느냐에 따라 이런 아티팩트가 줄어드거나 더 늘어나며 실제 필터의 설계와 선택에서는 이러한 아티팩트를 이해하고 줄이는 과정도 존재한다.[8] 예를 들어 신호 재구성에서 “싱크 함수 양단을 단순히 잘라내면 심각한 링잉 아태픽트가 발생”하며, 이런 아티팩트를 줄이기 위해 “양단이 더 부드럽게 감쇠되는 윈도우 함수”를 이용한다.[9]
시간 응답 [ 편집 ]
저주파 통과 필터의 시간 응답은 가장 간단한 1차 저주파 통과 필터인 RC 필터의 응답을 해석하여 풀 수 있다. 키르히호프의 전기회로 법칙으로 미분방정식을 세워 풀어낸 시간 응답은 다음과 같다.[10]
v out ( t ) = v in ( t ) − R C d ⁡ v out d ⁡ t {\displaystyle v_{\text{out}}(t)=v_{\text{in}}(t)-RC{\frac {\operatorname {d} v_{\text{out}}}{\operatorname {d} t}}}

예를 들어, 단위 계단 함수의 응답의 경우 계단 함수 v in ( t ) {\displaystyle v_{\text{in}}(t)} 의 크기가 V i {\displaystyle V_{i}} 인 경우 미분방정식의 해가 아래와 같이 나온다.[11]
v out ( t ) = V i ( 1 − e − ω 0 t ) {\displaystyle v_{\text{out}}(t)=V_{i}(1-e^{-\omega _{0}t})}

여기서 ω 0 = 1 R C {\displaystyle \omega _{0}={1 \over RC}} 는 필터의 차단 주파수이다.

주파수 응답 [ 편집 ]
주파수 응답을 구하는 가장 빠른 방법은 라플라스 변환[10] 전달 함수인 H ( s ) = V o u t ( s ) V i n ( s ) {\displaystyle H(s)={V_{\rm {out}}(s) \over V_{\rm {in}}(s)}} 를 구하는 것이다.

미분방정식에 라플라스 변환을 하여 H ( s ) {\displaystyle H(s)} 를 구하면 다음과 같다.

H ( s ) = V o u t ( s ) V i n ( s ) = ω 0 ( s + ω 0 ) {\displaystyle H(s)={V_{\rm {out}}(s) \over V_{\rm {in}}(s)}={\omega _{0} \over (s+\omega _{0})}}

이산 시간 샘플링의 미분방정식 [ 편집 ]
이산 선형 미분 방정식은 n = 0 , 1 , . . . {\displaystyle n=0,1,…} 의 이산 간격으로 T {\displaystyle T} 마다, 즉 n T {\displaystyle nT} 시간 만큼 샘플링하여 만들 수 있다. 샘플링된 두 신호의 차이는 다음과 같이 구할 수 있다.

v o u t ( n T ) − v o u t ( ( n − 1 ) T ) = V i ( 1 − e − ω 0 n T ) − V i ( 1 − e − ω 0 ( ( n − 1 ) T ) ) {\displaystyle v_{\rm {out}}(nT)-v_{\rm {out}}((n-1)T)=V_{i}(1-e^{-\omega _{0}nT})-V_{i}(1-e^{-\omega _{0}((n-1)T)})}

여기서 v o u t ( n T ) {\displaystyle v_{\rm {out}}(nT)} 를 구하면 다음과 같다.

v o u t ( n T ) = β v o u t ( ( n − 1 ) T ) + ( 1 − β ) V i {\displaystyle v_{\rm {out}}(nT)=\beta v_{\rm {out}}((n-1)T)+(1-\beta )V_{i}}

여기서 β = e − ω 0 T {\displaystyle \beta =e^{-\omega _{0}T}} 이다.

위 식에서 V n = v o u t ( n T ) {\displaystyle V_{n}=v_{\rm {out}}(nT)} , v n = v i n ( n T ) {\displaystyle v_{n}=v_{\rm {in}}(nT)} 으로 대입하고 샘플링한 값인 v n = V i {\displaystyle v_{n}=V_{i}} 를 대입하면 아래와 같은 미분방정식을 얻을 수 있다.

V n = β V n − 1 + ( 1 − β ) v n {\displaystyle V_{n}=\beta V_{n-1}+(1-\beta )v_{n}}

전기 회로 [ 편집 ]
1차 필터 [ 편집 ]
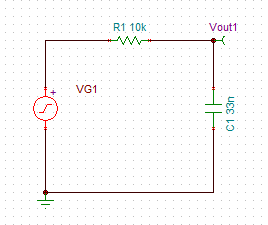
1차 수동 저주파 통과 필터인 RC 회로.

전기 회로로 만든 대표적인 1차 저주파 통과 필터는 부하와 저항기를 직렬로 연결하고 축전기를 병렬로 연결하여 만든다. 이를 RC 필터라고 한다. 축전기는 리액턴스를 가져 저주파 신호를 차단하여 부하로 저주파가 가도록 한다. 높은 주파수에서는 리액턴스가 감소하므로 캐피시터가 사실상 단락시킨다. 저항기와 축전기가 합쳐져서 필터에는 시간 상수 τ = R C {\displaystyle \scriptstyle \tau \;=\;RC} 가 존재한다. 차단 주파수는 바로 이 시간 상수에 따라 결정된다.

f c = 1 2 π τ = 1 2 π R C {\displaystyle f_{\mathrm {c} }={1 \over 2\pi \tau }={1 \over 2\pi RC}}

단위를 rad/s로 바꿀 경우 다음과 같다.

ω c = 1 τ = 1 R C {\displaystyle \omega _{\mathrm {c} }={1 \over \tau }={1 \over RC}}

1차 필터는 RC 필터 외에도 저항기와 인덕터를 결합한 RL 회로로도 만들 수 있다. 1차 RL 필터는 저항 1개와 인덕터 1개로 구성되며 가장 간단한 아날로그 무한 임펄스 응답 전자 필터 중 하나이다.

같이 보기 [ 편집 ]
하이패스 필터 (고주파 통과 필터, HPF)

각주 [ 편집 ]

So you have finished reading the 1 차 저역 통과 필터 topic article, if you find this article useful, please share it. Thank you very much. See more: 2차 저역통과필터, 능동 저역 통과 필터, LPF 필터, 1차 low pass filter, 로우패스필터 코드, 저역통과필터 차단주파수, Low Pass filter 수식, 저역통과필터 원리

1차 Low-Pass Filter(저주파 통과필터), High-Pass Filter(고주파 통과 필터) 구현하기, 코드

1차 수동 필터 – 저역 통과 필터(LPF), 고역통과필터(HPF) : 네이버 블로그

[회로 기초] 능동 저역통과 필터(Low-pass filter)에 대해 알아보자

로우패스 필터 – 위키백과, 우리 모두의 백과사전

1차 LPF [정보통신기술용어해설]

[필터연재] 1차 디지털 저역/고역 통과필터

[필터연재] 1차 디지털 저역/고역 통과필터

RC Low pass filter (LPF)란?

1차 Low-Pass Filter(저주파 통과필터), High-Pass Filter(고주파 통과 필터) 구현하기, 코드

[회로 기초] 능동 저역통과 필터(Low-pass filter)에 대해 알아보자

위키백과, 우리 모두의 백과사전

Leave a Comment Cancel reply